Questão 177 – Trigonometria
Um grupo de engenheiros está projetando um motor cujo esquema de deslocamento vertical do pistão dentro da câmara de combustão está representado na figura.
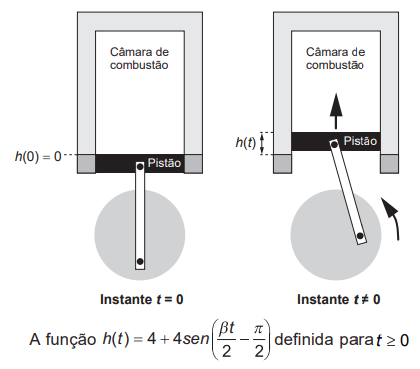
descreve como varia a altura h, medida em centímetro, da parte superior do pistão dentro da câmara de combustão, em função do tempo t, medido em segundo. Nas figuras estão indicadas as alturas do pistão em dois instantes distintos.
O valor do parâmetro β, que é dado por um número inteiro positivo, está relacionado com a velocidade de deslocamento do pistão. Para que o motor tenha uma boa potência, é necessário e suficiente que, em menos de 4 segundos após o início do funcionamento (instante t = 0), a altura da base do pistão alcance por três vezes o valor de 6 cm.
Para os cálculos, utilize 3 como aproximação para π.
O menor valor inteiro a ser atribuído ao parâmetro β, de forma que o motor a ser construído tenha boa potência, é
A) 1.
B) 2.
C) 4.
D) 5.
E) 8.
Solução
O enunciado nos diz que para que o motor tenha uma boa potência ele tem que atingir a altura de 6 cm no tempo t menor que 4 segundos.
Vamos substituir na equação h(t) = 6
6 = 4 + 4.sen(Bt/2 – π/2)
2 = 4.sen(Bt/2 – π/2)
1/2 = sen(Bt/2 – π/2)
Sabemos que sen(π/6) = 1/2, como o enunciado pede pela terceira vez temos que analisar o círculo trigonométrico para concluir que a primeira é em π/6, a seguinte é em 5π/6 e a terceira em 2π + π/6 então temos que
2π + π/6 = Bt/2 – π/2
Como pi = 3
6 + 3/6 = Bt/2 – 3/2
6 + 1/2 + 3/2 = Bt/2
6 + 2 = Bt/2
8 = Bt/2
Bt = 16
t = 16/B
Como t < 4,
16/B < 4
B > 4
O menor valor inteiro maior que 4 é 5.
Alternativa D
Veja a resolução com mais detalhes no vídeo abaixo!






