Questão 139 – Geometria Plana
Sobre um sistema cartesiano considera-se uma malha formada por circunferências de raios com medidas dadas por números naturais e por 12 semirretas com extremidades na origem, separadas por ângulos de π/6 rad conforme a figura.
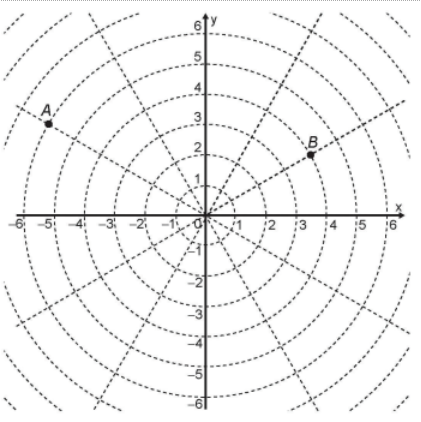
Suponha que os objetos se desloquem apenas pelas semirretas e pelas circunferências dessa malha, não podendo passar pela origem (0;0).
Considere o valor de π com aproximação de, pelo menos, uma casa decimal.
Para realizar o percurso mais curto possível ao longo da malha, do ponto B até o ponto A, um objeto deve percorrer uma distância igual a:
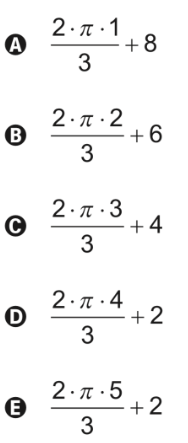
Solução
O menor caminho será o que utiliza a maior quantidade de reta possível e a menor circunferência possível
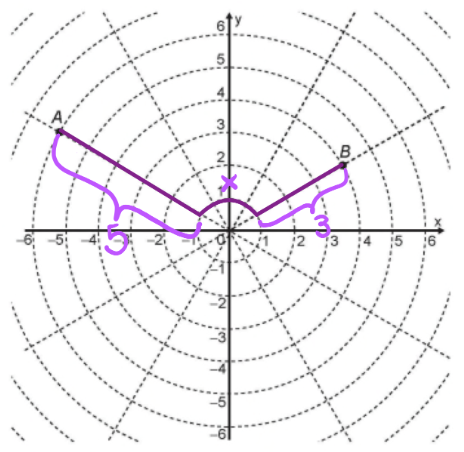
A parte x da circunferência de raio 1 é dada por
1.4.π/6 = π/2
O comprimento do percurso total é a soma
5 + 3 + 2π/3 = 8 + 2.π.1/3
Alternativa A
Veja a resolução com mais detalhes no vídeo abaixo!






