Um tanque, em formato de paralelepípedo reto retângulo, tem em seu interior dois anteparos verticais, fixados em sua base e em duas paredes opostas, sendo perpendiculares a elas, conforme a figura.

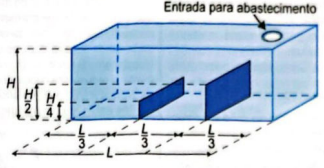
Esses anteparos, de espessuras desprezíveis, estão instalados de maneira a dividir a base do tanque em três retângulos congruentes, tendo suas alturas iguais à metade e a um quarto da altura do tanque. O tanque é abastecido por uma entrada situada no teto, através de um duto que despeja água a uma vazão constante, sendo necessárias 12 horas para finalizar o seu enchimento.

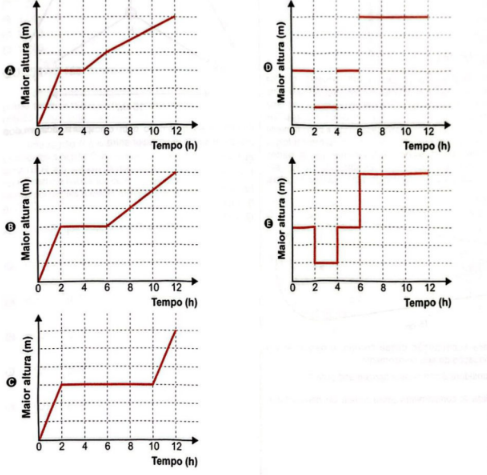
Resolução 

Como o gráfico precisa descrever qual a maior altura da água durante o enchimento, nota-se que para encher o primeiro compartimento a água irá alcançar metade da altura do tanque. Sendo esse primeiro momento representado por uma reta crescente inclinada para a direita até alcançar H/2. 

Após isso, por mais que continue a encher os outros compartimentos, a maior altura ainda permanece sendo H/2 até que encha completamente o tanque à metade. Sendo assim, o gráfico da altura, ficará representado por uma reta constante sem variação.

E, por fim, a uma vazão constante, o restante do tanque será enchido até completar a altura máxima H, sendo esse momento representado no gráfico como uma reta inclinada para direita.

Com isso, eliminamos as alternativas D e E. E para diferenciarmos as outras alternativas, precisamos encontrar em quanto tempo foi enchido cada compartimento. Para isso, é preciso levar em consideração que a vazão é constante, sendo assim, se é gasto 12 horas para encher o tanque por completo, sabemos que a metade dele gastaria 6 horas. Com isso, eliminamos a letra C.

Da mesma forma, sabemos que se foi gasto 2 horas para encher o primeiro compartimento, como ele era equivalente e ⅓ da metade da altura, a reta deveria ficar constante por mais 4 horas, até a água atingir completamente a metade da capacidade do tanque. Sendo então a alternativa B a correta.

Alternativa B