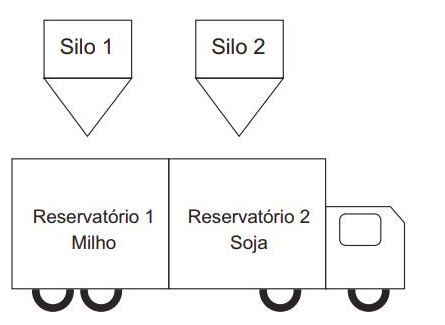
Um pequeno caminhão dispõe de dois reservatórios vazios, cada um com capacidade de 2 000 kg, os quais serão utilizados para transportar a produção de milho e soja até um centro consumidor. No centro de abastecimento abre-se o registro de um primeiro silo às 12 horas para alimentar o reservatório 1 com milho, numa taxa de 120 kg por minuto. Passados cinco minutos, abre-se o registro de um segundo silo para alimentar o reservatório 2 com soja, numa taxa de 80 kg por minuto. Considere que a encomenda de milho no centro consumidor seja de 1 800 kg e que, pela lei rodoviária local, a carga máxima a ser transportada por caminhão seja de 3 400 kg.
Nestas condições, em que instantes devem ser fechados os registros dos silos 1 e 2, respectivamente, para que a quantidade de soja transportada seja a máxima possível?
A) 12h15min e 12h20min
B) 12h15min e 12h25min
C) 12h15min e 12h27min30seg
D) 12h15min e 12h30min
E) 12h15min e 12h32min30seg
Solução
Para que a carga seja a maior possível, deve ser igual a 3400 kg permitidos pela lei. Como é dito que a encomenda de milho foi de 1800 kg, a quantidade de soja deve ser: 3400 – 1800 = 1600 kg.
Sendo assim, agora sabendo a quantidade de cada, iremos calcular em que instante cada silo deve ser fechado:
Silo 1: abre 12:00 e libera 120 kg por minuto, sendo assim:
1min —– 120 kg
x min ——- 1800 kg
120x = 1800
x = 15 min
Ou seja, o silo 1 deve fechar 12h15min
Silo 2: abre 12:05 e libera 80 kg por minuto, sendo assim:
1min —— 80 kg
x min —— 1600 kg
80x = 1600
x = 20 min
Ou seja, o silo 2 deve fechar 12h25min
Alternativa B






