Uma microempresa pretende fabricar pipas para vender no próximo verão. Um modelo de pipa está representado pelo quadrilátero ABCD.
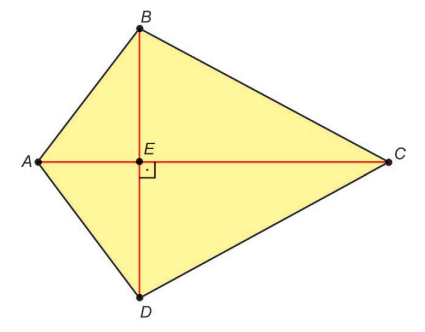
Nessa representação, os segmentos AB, BC e CE medem, respectivamente, 20 cm, 34 cm e 30 cm. Além disso, E pertence ao segmento AC e é ponto médio do segmento BD.
A medida da área, em centímetro quadrado, desse modelo de pipa é
A) 58.
B) 96.
C) 108.
D) 184.
E) 672.
Solução
Para resolvermos essa questão, basta notarmos que BEC formam um triângulo retângulo, como sabemos a medida de BC e CE podemos calcular o valor de EB por pitágoras, ficando:
34² = 30² + x²
1156 = 900 + x²
256 = x²
16 = x
Sabendo que o lado EB vale 16, temos que o lado ED, também, vale 16 e como o triângulo ABE também é retângulo conseguimos descobrir a medida de AE, fazendo:
20² = 16² + y²
400 = 256 + y²
144 = y²
12 = y
Sabendo essas medidas, conseguimos calcular a área total dessa pipa, pois ao separá-lo em 2 triângulos, sendo o triângulo DAB e DBC, conseguimos calcular a área de cada um deles, pela fórmula da área de triângulos:
A = 32 . 12 / 2 + 32 . 30 / 2
A = 192 + 480
A = 672 cm²
Alternativa E






