O proprietário de um terreno retangular medindo 10 m por 31,5 m deseja instalar lâmpadas nos pontos C e D, conforme ilustrado na figura:
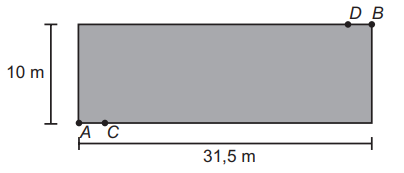
Cada lâmpada ilumina uma região circular de 5 m de raio. Os segmentos AC e BD medem 2,5 m. O valor em m² mais aproximado da área do terreno iluminada pelas lâmpadas é (Aproxime √3 para 1,7 e π para 3.)
A) 30.
B) 34.
C) 50.
D) 61.
E) 69.
Resolução
Nessa questão é preciso se atentar ao fato de que a lâmpada ilumina uma região circular de 5 cm de raio, porém, como AC e BD têm 2,5 a área iluminada perto a esses pontos formará um triângulo retângulo, como o representado abaixo:
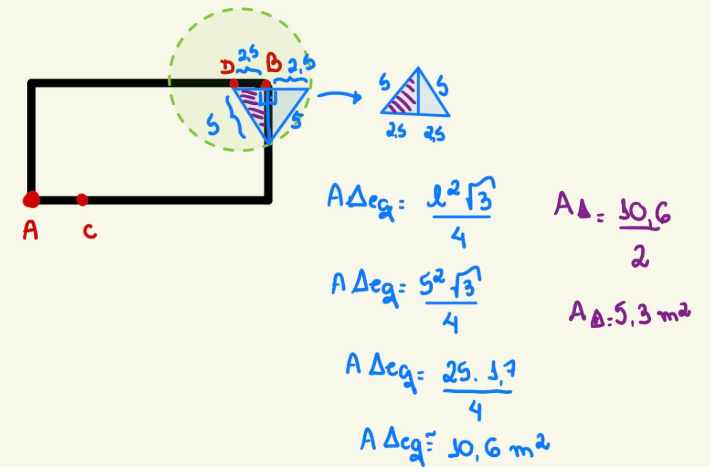
Após encontrarmos que a área iluminada no triângulo corresponde a 5,3 m² precisamos encontrar, qual a área do setor circular restante que a lâmpada ilumina, para isso, precisamos descobrir qual o ângulo desse setor circular. Como sabemos que o triângulo ao lado é equilátero, ele tem todos os ângulos iguais a 60º, sendo assim, fica fácil descobrir a área do setor circular, basta acompanhar a ilustração abaixo:
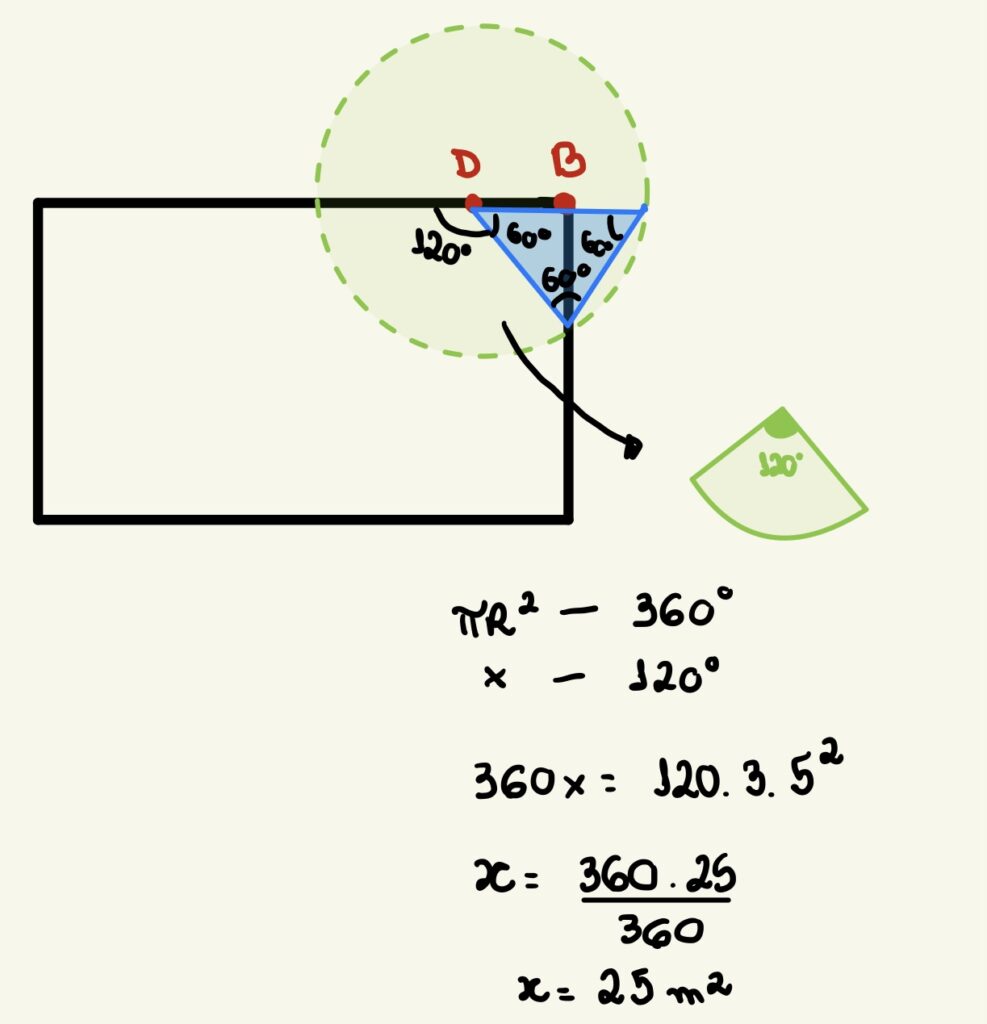
Portanto, sabemos que cada lâmpada ilumina uma área de 25 + 5,3 = 30,3 m². Como temos duas lâmpadas, a área total iluminada será de 60,6 m².
Alternativa D






