Em uma casa, há um espaço retangular medindo 4 m por 6 m, onde se pretende colocar um piso de cerâmica resistente e de bom preço. Em uma loja especializada, há cinco possibilidades de pisos que atendem às especificações desejadas, apresentadas no quadro:
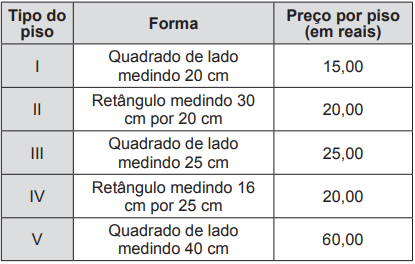
Levando-se em consideração que não há perda de material, dentre os pisos apresentados, aquele que implicará o menor custo para a colocação no referido espaço é o piso:
A) I.
B) II.
C) III.
D) IV.
E) V.
Resolução
Para determinar qual piso resulta no menor custo para cobrir o espaço de 4 m por 6 m, precisamos calcular o número de peças necessárias de cada tipo de piso e o custo total correspondente. Sabendo que a área total do espaço é 4 . 6 = 24 m² faremos uma análise de cada tipo de piso:
Piso I: Quadrado de lado 20 cm (0,2 m).
- Área de cada peça: 0,2 . 0,2 = 0,04 m².
- Número de peças necessárias: 24 ÷ 0,04 = 600 peças.
- Custo total: 600 . 15,00 = R$ 9.000,00.
Piso II: Retângulo de 30 cm por 20 cm (0,3 m × 0,2 m).
- Área de cada peça: 0,3 . 0,2 = 0,06 m².
- Número de peças necessárias: 24 ÷ 0,06 ≈ 400 peças.
- Custo total: 400 . 20,00 = R$ 8.000,00.
Piso III: Quadrado de lado 25 cm (0,25 m).
- Área de cada peça: 0,25 . 0,25 = 0,0625 m².
- Número de peças necessárias: 24 ÷ 0,0625 = 384 peças.
- Custo total: 384 . 25,00 = R$ 9.600,00.
Piso IV: Retângulo de 16 cm por 25 cm (0,16 m × 0,25 m).
- Área de cada peça: 0,16 . 0,25 = 0,04 m².
- Número de peças necessárias: 24 ÷ 0,04 = 600 peças.
- Custo total: 600 . 20,00 = R$ 12.000,00.
Piso V: Quadrado de lado 40 cm (0,4 m).
- Área de cada peça: 0,4 × 0,4 = 0,16 m².
- Número de peças necessárias: 24 ÷ 0,16 = 150 peças.
- Custo total: 150 × 60,00 = R$ 9.000,00.
Portanto, concluímos que o Piso II resulta no menor custo total de R$ 8.000,00 para cobrir o espaço de 24 m².
Alternativa B






