Em um ano, uma prefeitura apresentou o relatório de gastos públicos realizados pelo município. O documento mostra que foram gastos 72 mil reais no mês de janeiro (mês 1), que o maior gasto mensal ocorreu no mês de agosto (mês 8) e que a prefeitura gastou 105 mil reais no mês de dezembro (mês 12). A curva que modela esses gastos é a parábola y = T(x), com x sendo o número correspondente ao mês e T(x), em milhar de real.
A expressão da função cujo gráfico é o da parábola descrita é
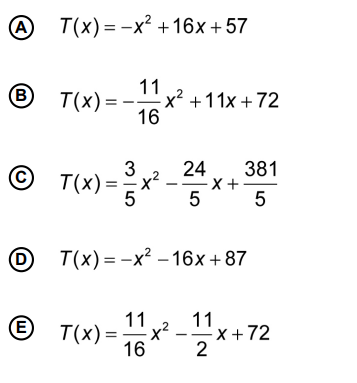
Resolução
Para resolvermos essa questão, precisamos observar que no enunciado é mencionado os pares ordenados pertencentes a questão: (1 , 72) e ( 12,105). Além disso, ao dizer que a função possui um ponto máximo, sabemos que se trata de uma parábola com a concavidade para baixo e o termo A negativo. Sendo também o Xv igual a 8.
Com isso, pela fórmula de Xv temos que:
Xv = -b/2a
8 = – b / 2a
– 16a = b
Substituindo os pares ordenados na função de segundo grau temos:
(1,72) (12, 105)
y = ax² + bx + c y = ax² + bx + c
72 = 1²a + (-16a).1 + c 105 = a . 12² + (-16a) . 12 + c
72 = 1a -16a + c 105 = 144a – 192a + c
72 = -15 a + c 105 = -48a + c
Utilizando soma de equações, temos:
105 = -48a + c
72 = -15 a + c . (-1)
105 = -48a + c
-72 = 15a – c
33 = – 33a
a = -1
Retornado na equação anterior, temos:
72 = -15a + c
72 = -15 . -1 + c
72 – 15 = c
57 = c
E, ainda temos que b = -16a = -16 . -1 = 16
Ficando a função igual a:
-x² + 16x + 57 = t(x)
Alternativa A






