Uma fábrica de tubos acondiciona tubos cilíndricos menores dentro de outros tubo cilíndricos. A figura mostra uma situação em que quatro tubos cilíndricos estão acondicionados perfeitamente em um tubo com raio maior.
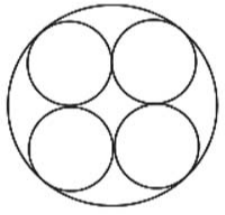
Suponha que você seja o operador da máquina que produzirá os tubos maiores em que serão colocados, sem ajustes ou folgas, quatro tubos cilíndricos internos.
Se o raio da base de cada um dos cilindros menores for igual a 6 cm, a máquina por você operada deverá ser ajustada para produzir tubos maiores, com raio da base igual a
A) 12 cm.
B) 12 √2 cm.
C) 24 √2 cm.
D) 6(1+√2) cm.
E) 12(1+√2) cm.
Solução
Para encontrar o valor do raio da circunferência maior, é necessário descobrir o espaço que está faltando no centro das circunferências menores. Podemos enxergar o seguinte triângulo na imagem:
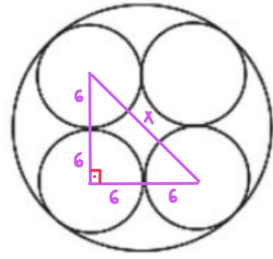
Para encontrar X, podemos aplicar o teorema de pitágoras, já que temos o valor de dois catetos (12)
X² = 12² + 12²
X² = 288
X = 122
Logo, o diâmetro da circunferência será igual a hipotenusa encontrada somada aos raios das circunferências menores:
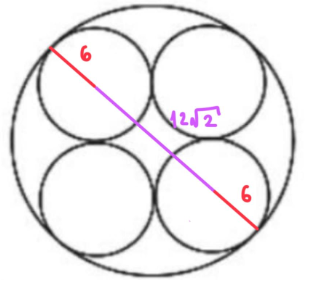
Diâmetro = 6 + 122 + 6 = 12 + 122
O comando pede o raio e o raio é igual a metade do diâmetro, portanto:
Raio = (12 + 122) / 2
Raio = 6 + 62
Colocando em evidência
6 + 62 = 6 (1 + 2 )
Alternativa D






