Um lapidador recebeu de um joalheiro a encomenda para trabalhar em uma pedra preciosa cujo formato é o de uma pirâmide, conforme ilustra a Figura 1. Para tanto, o lapidador fará quatro cortes de formatos iguais nos cantos da base. Os cantos retirados correspondem a pequenas pirâmides, nos vértices P, Q, R e S, ao longo dos segmentos tracejados, ilustrados na Figura 2.
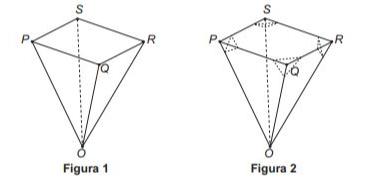
Depois de efetuados os cortes, o lapidador obteve, a partir da pedra maior, uma joia poliédrica cujos números de faces, arestas e vértices são, respectivamente, iguais a
A) 9, 20 e 13.
B) 9, 24 e 13.
C) 7, 15 e 12.
D) 10, 16 e 5.
E) 11, 16 e 5.
Solução
O sólido representado possuía 5 faces, 8 arestas e 5 vértices
Após os cortes, surgiram 4 novas faces no lugar das 4 vértices da base. Com isso, temos agora 9 faces.
No lugar de cada uma dessas vértices, surgiram novas 3, ou seja, temos 12 novas vértices na base do sólido, além da vértice da ponta da pirâmide, o que contabiliza 13 vértices ao todo.
De forma semelhante, o mesmo acontece com as arestas. Surgem novas 3 para cada ponta da base, isso significa dizer que, além das 8 já existentes, agora temos 8 + 12 = 20 arestas
Faces: 9
Arestas: 20
Vértices: 13
Alternativa A






