Um terreno retangular de lados cujas medidas, em metro, são x e y será cercado para a construção de um parque de diversões. Um dos lados do terreno encontra-se às margens de um rio. Observe a figura.
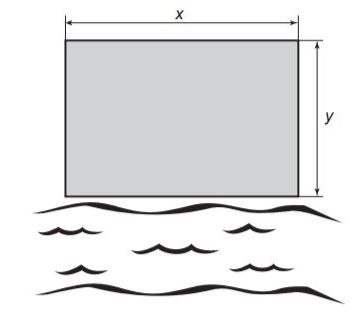
Para cercar todo o terreno, o proprietário gastará R$ 7 500,00. O material da cerca custa R$ 4,00 por metro para os lados do terreno paralelos ao rio, e R$ 2,00 por metro para os demais lados.
Nessas condições, as dimensões do terreno e o custo total do material podem ser relacionados pela equação
A) 4(2x + y) = 7 500
B) 4(x + 2y) = 7 500
C) 2(x + y) = 7 500
D) 2(4x + y) = 7 500
E) 2(2x + y) = 7 500
Solução
Para resolvermos essa questão, precisamos observar que para cercar todo o terreno é necessário 2x m e 2y m. Como é dito que cada metro paralelo ao rio custa R$ 4,00 temos, então, que o valor gasto nos lados x é 4 . 2x = 8x . Além disso, é dito que o outro lado do terreno custa 2 . 2y = 4y.
Sendo assim, como o gasto total é R$ 7.500, temos a equação da soma dos gastos igual a:
8x + 4y = 7500
4(2x + y) = 7500
Alternativa A






