Dispondo de um grande terreno, uma empresa de entretenimento pretende construir um espaço retangular para shows e eventos, conforme a figura.
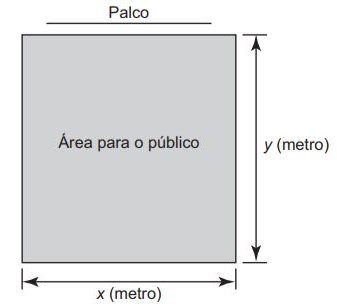
A área para o público será cercada com dois tipos de materiais:
• nos lados paralelos ao palco será usada uma tela do tipo A, mais resistente, cujo valor do metro linear é R$ 20,00;
• nos outros dois lados será usada uma tela do tipo B, comum, cujo metro linear custa R$ 5,00.
A empresa dispõe de R$ 5 000,00 para comprar todas as telas, mas quer fazer de tal maneira que obtenha a maior área possível para o público.
A quantidade de cada tipo de tela que a empresa deve comprar é
A) 50,0 m da tela tipo A e 800,0 m da tela tipo B.
B) 62,5 m da tela tipo A e 250,0 m da tela tipo B.
C) 100,0 m da tela tipo A e 600,0 m da tela tipo B.
D) 125,0 m da tela tipo A e 500,0 m da tela tipo B.
E) 200,0 m da tela tipo A e 200,0 m da tela tipo B.
Solução
Para resolvermos essa questão, temos que saber que a área de um retângulo pode ser calculada pela fórmula A = x·y, onde x e y são os lados do retângulo. Neste problema, o lado x será cercado com um tipo de cerca que custa R$20 por metro, enquanto o lado y será cercado com outro tipo de cerca que custa R$5 por metro.
O custo total para cercar o perímetro do terreno é dado por:
C = 20x + 20x + 5y + 5y, que pode ser simplificado para:
C = 40x + 10y
Sabemos que o orçamento máximo disponível para cercar o terreno é de R$5000. Assim, temos a equação:
5000 = 40x + 10y
Simplificando os valores e isolando o y na equação:
y = 500 – 4x
Agora substituímos essa expressão de y na fórmula da área do retângulo:
A = x·y
A = x·(500 – 4x)
A = -4x² + 500x
Como queremos maximizar a área, precisamos encontrar o valor de x no vértice da parábola representada por essa equação. Para isso, usamos a fórmula do vértice:
Xv = -b/2a, onde a = -4 e b = 500. Substituímos os valores:
Xv = -500/2•(-4)
Xv = 62,5
Com x = 62,5, calculamos y substituindo na equação y = 500 – 4x:
y = 500 − 4•62,5
y = 250
Portanto, os lados do retângulo que maximizam a área são x = 62,5 m e y = 250 m.
Como o retângulo tem dois lados iguais de cada tipo, precisamos de:
125 metros de cerca A (R$20/m) para os dois lados com medida x;
500 metros de cerca B (R$5/m) para os dois lados com medida y.
Alternativa D






