Uma região de uma fábrica deve ser isolada, pois nela os empregados ficam expostos a riscos de acidentes. Essa região está representada pela porção de cor cinza (quadrilátero de área S) na figura.
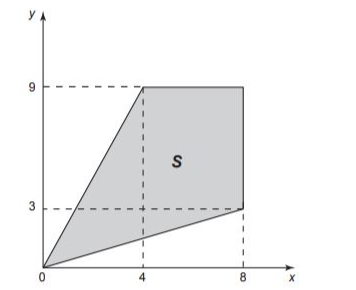
Para que os funcionários sejam orientados sobre a localização da área isolada, cartazes informativos serão afixados por toda fábrica. Para confeccioná-los, um programador utilizará um software que permite desenhar essa região a partir de um conjunto de desigualdades algébricas.
As desigualdades que devem ser utilizadas no referido software, para o desenho da região de isolamento, são
A) 3y – x ≤ 0; 2y – x ≥ 0; y ≤ 8; x ≤ 9
B) 3y – x ≤ 0; 2y – x ≥ 0; y ≤ 9; x ≤ 8
C) 3y – x ≥ 0; 2y – x ≤ 0; y ≤ 9; x ≤ 8
D) 4y – 9x ≤ 0; 8y – 3x ≥ 0; y ≤ 8; x ≤ 9
E) 4y – 9x ≤ 0; 8y – 3x ≥ 0; y ≤ 9; x ≤ 8
Solução
Para resolvermos essa questão, vamos considerar o segmento BC como referência, sabemos que:
x ≤ 8
Já para o segmento AB, temos:
y ≤ 9
Agora, analisando a reta AO, sabemos que ela passa pela origem e, portanto, sua equação será da forma:
y = mx
Para determinar o valor de m, usamos o fato de que a reta passa pelo ponto (4, 9). Assim:
9 = m·4
m = 9/4
Com isso, a equação da reta será:
y = (9/4)x
Podemos reescrever essa equação na forma padrão:
y – (9/4)x ≤ 0
Multiplicando todos os termos por 4 para eliminar o denominador:
4y – 9x ≤ 0
Alternativa E






