Em um trabalho escolar, João foi convidado a calcular as áreas de vários quadrados diferentes, dispostos na sequência, da esquerda para a direita, como mostra a figura.
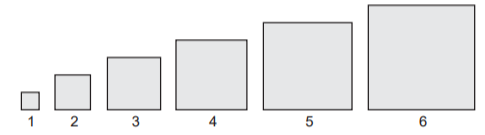
O primeiro quadrado da sequência tem lado medindo 1 cm, o segundo quadrado tem lado medindo 2 cm, o terceiro quadrado tem lado medindo 3 cm e assim por diante. O objetivo do trabalho é identificar em quanto a área de cada quadrado da sequência excede a área do quadrado anterior. A área do quadrado que ocupa a posição n, na sequência foi representada por An.
Para n ≥ 2, o valor da diferença An – An–1, em centímetro quadrado, é igual a
A) 2n – 1
B) 2n + 1
C) –2n + 1
D) (n – 1)²
E) n² – 1
Solução
O comando pede a diferença da área de An – An-1, assim, sabendo que, a área de um quadrado (An) é igual a n² para a encontrar a área de An-1 devemos subtrair 1, ou seja, (n-1)².
Montando a relação temos:
n² – (n-1)²
n²-( n² -2n +1)
n² – n² + 2n -1
2n -1
Alternativa A






