Finalmente entenda Análise Combinatória para o ENEM!

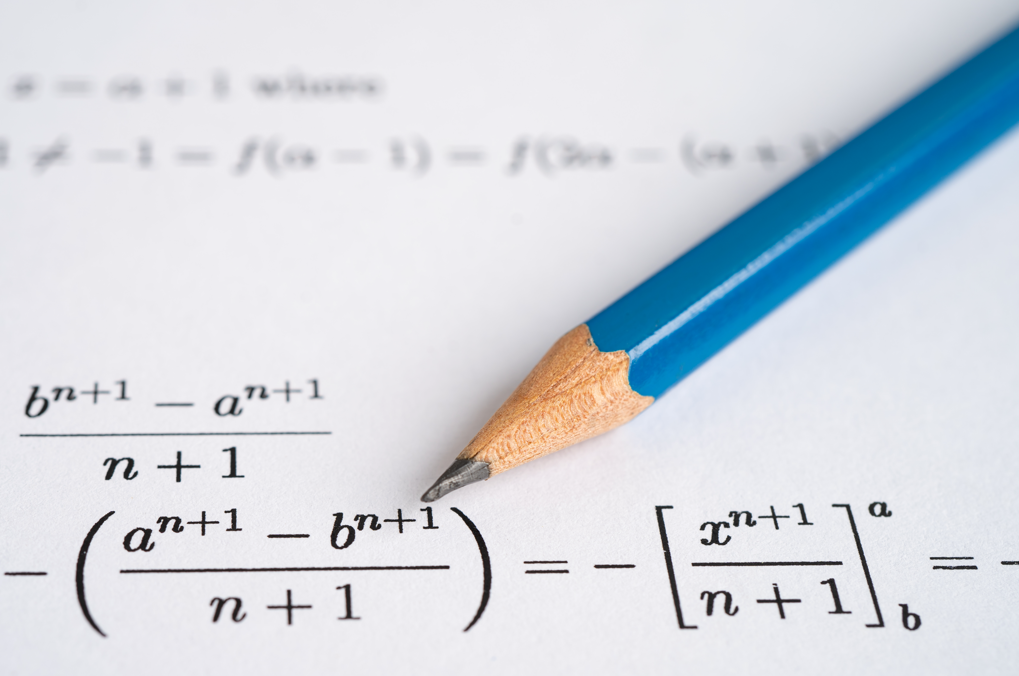
O que é Análise Combinatória?

Análise combinatória é um conjunto de técnicas matemáticas usadas para contar quantas maneiras diferentes podemos agrupar ou organizar elementos dentro de um conjunto.

Ela é amplamente aplicada em problemas de probabilidade, lógica e contagem. No ENEM, apesar de não ser recorrente todos os anos, é um tema que exige atenção, pois permite inúmeras possibilidades de questões.

Conteúdos que você precisa dominar

Estes são os tópicos mais importantes:

• Fatorial
• Princípio Fundamental da Contagem
• Permutação Simples
• Permutação com Repetição
• Arranjo Simples
• Combinação Simples
• Princípios Aditivo e Multiplicativo

Vamos entender cada um com exemplos práticos!

Fatorial

O fatorial (n!) é a base para quase todos os cálculos combinatórios. Ele é o produto de um número natural por todos os seus antecessores positivos:

• 1! = 1
• 2! = 2 × 1 = 2
• 3! = 3 × 2 × 1 = 6
• 4! = 4 × 3 × 2 × 1 = 24
• 5! = 5 × 4 × 3 × 2 × 1 = 120

Princípio Fundamental da Contagem

Se um evento pode ocorrer de m maneiras e outro de n, então o total de possibilidades é:

Total = m × n

Exemplo: Jeniffer quer comprar uma saia. A loja tem 3 modelos e 4 cores. Quantas opções ela tem?

Total = 3 (modelos) × 4 (cores) = 12

Permutação Simples (sem repetição)

Usada quando a ordem importa e não há repetição de elementos.

P = n!

Exemplo: Quantos anagramas dá para formar com a palavra AMOR?

AMOR tem 4 letras distintas:

P = 4! = 24

Permutação com Repetição

Usada quando alguns elementos se repetem.

Fórmula:

P_n = n! / (n₁! × n₂! × … × n_k!)

n! = Quantidade dos elementos do evento
n₁! × n₂! × … × n_k! = Elementos repetidos do evento

Exemplo: Quantos anagramas com a palavra CASA?

A palavra tem 4 letras, mas o “A” se repete:

P = 4!/2! = 24/2 = 12

Arranjo Simples

Usado quando a ordem importa, mas não usamos todos os elementos.

Fórmula:

A_(n,p) = n!/(n – p)!

A = Arranjo
n = elementos
p = Agrupamentos

Exemplo: Quantas formas de premiar 3 entre 4 alunos?

A_(4,3) = 4! / (4 – 3)! = 24

Combinação Simples

Usada quando a ordem não importa.

Fórmula:

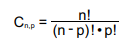
C = Combinação
n = Elementos
p = Agrupamento
Sendo sempre: p ≤ n

Exemplo: De quantas formas posso escolher 2 bolinhas de um total de 10?

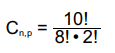
Princípios Básicos de Contagem

1. Princípio Aditivo (OU)

Usado quando se trata de escolhas mutuamente exclusivas.

Exemplo: Escolher 2 livros de matemática ou 2 de português:

C(4,2) + C(3,2)

2. Princípio Multiplicativo (E)

Usado quando as ações são encadeadas.

Exemplo: Um livro de matemática e um de português:

C(4,1) × C(3,1)

Dicas Finais para o ENEM

• Identifique rapidamente se a ordem importa (permutações e arranjos) ou não importa (combinações).
• Sempre que houver repetição de elementos, use o fatorial com divisões.
• Use o Princípio Fundamental da Contagem como plano B para raciocinar casos que não se encaixam perfeitamente nas fórmulas.

Saber trabalhar com Análise combinatória é fundamental para resolver questões de forma rápida e correta no ENEM.

No extensivo xequemat você tem acesso a aulas gravadas sobre esse assunto e todos os outros que ja caíram no ENEM com exercícios focados no exame! Se você busca se destacar dos seus concorrentes e aumentar as suas chances de entrar no seu curso dos sonhos faça parte agora mesmo!