Questão 143 – ENEM PPL 2011

Um programador visual deseja modificar uma imagem, aumentando seu comprimento e mantendo sua largura. As figuras 1 e 2 representam, respectivamente, a imagem original e a transformada pela duplicação do comprimento. 

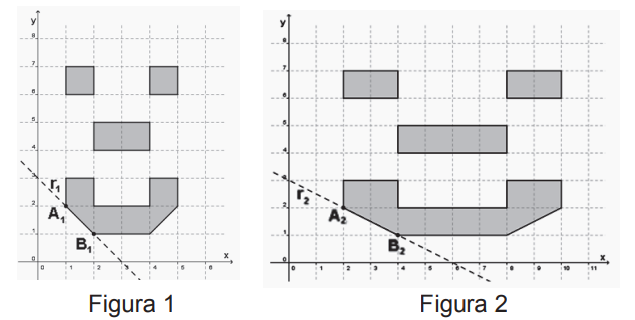
Para modelar todas as possibilidades de transformação no comprimento dessa imagem, o programador precisa descobrir os padrões de todas as retas que contêm os segmentos que contornam os olhos, o nariz e a boca e, em seguida, elaborar o programa. 

No exemplo anterior, o segmento A1 B1 da figura 1, contido na reta r₁ , transformou-se no segmento A₂ B₂ da figura 2, contido na reta r₂ . 

Suponha que, mantendo constante a largura da imagem, seu comprimento seja multiplicado por n, sendo n um número inteiro e positivo, e que, dessa forma, a reta r₁ sofra as mesmas transformações. Nessas condições, o segmento A_n B_n estará contido na reta r_n .

A equação algébrica que descreve r_n , no plano cartesiano, é 

A) x + ny = 3n. 

B) x − ny = − n. 

C) x − ny = 3n. 

D) nx + ny = 3n. 

E) nx + 2ny = 6n.

Solução

Para resolvermos essa questão, basta observarmos que a reta r1 intercepta o eixo y no ponto (0,3) e o eixo x no ponto (3,0). Após ter tido seu comprimento duplicado na figura 2, observamos que na reta r2, o ponto que intercepta o eixo y permanece o mesmo, pois a largura a figura não pode se alterar, mas o ponto que intercepta o eixo x, também foi duplicado, passando de (3,0) para ( 6,0). 

Sendo assim, podemos concluir que, se o comprimento da figura for multiplicado por n, a reta r_n,  vai interceptar o eixo x, no ponto (3n, 0) e o eixo y irá se manter interceptado no ponto (0,3).

Com isso, para obtermos a equação da reta r_n, podemos utilizar o método TGH, substituindo os pontos encontrados da reta r_n,  nas alternativas dadas pela questão.

Ou seja, temos os pontos (3n , 0) e vamos substituí-lo nas alternativas, sendo x= 3n e y = 0. 

a: 3n + n.0 = 3n

                          3n = 3n     (deu certo)

b: 3n – n.0 = -n

                         3n = -n            (errada a igualdade)

c: 3n – n.0 = 3n

                          3n = 3n           (deu certo)

d: 3n.n + n.0 = 3n

                         3n² = 3n           (errada a igualdade)

e: 3n.n + 2n.0 = 6n

                         3n² = 6n          (errada a igualdade)

Como as alternativas a e c deram certo, utilizaremos o segundo ponto pertence a reta  r_n  para podermos identificar qual está correta. Usando o par ordenado (0,3)

a: 0 + n.3 =3n

                        3n = 3n

c: 0 – n . 3 = 3n

              -3n = 3n ( a igualdade não corresponde)

Portanto, a equação que descreve a reta r_n  é a da alternativa A.

Alternativa A