Um administrador de um campo de futebol deseja recobri-lo com um tipo de grama que, em condições normais, cresce de acordo com o gráfico a seguir.
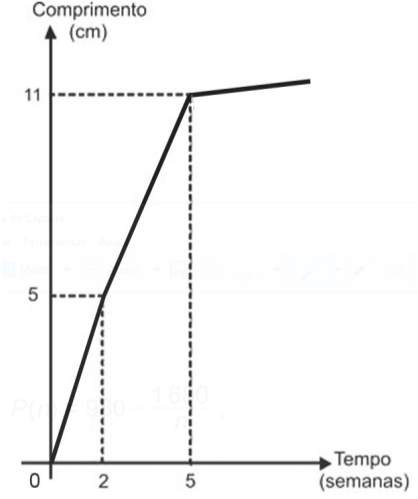
Ele precisa ter o campo pronto no dia 11 de junho de 2012, e o comprimento mínimo da grama nesse dia deve ser igual a 7 cm.
Supondo-se que o crescimento da grama se dê em condições normais, a grama deve ser plantada, no máximo, até o dia
A) 17 de maio de 2012.
B) 21 de maio de 2012.
C) 23 de maio de 2012.
D) 8 de junho de 2012.
E) 9 de junho de 2012.
Solução
Para resolvermos essa questão basta calcularmos montarmos uma regra de 3, a partir dos dados fornecidos no gráfico, onde calculamos a variação do primeiro par ordenado (2,5), em relação ao par ordenado (5,11) e depois a variação do que nós queremos encontrar (2,5) em relação ao (x,7). Ficando:
6 —— 3
2 —— x
6x = 6
x = 1 semana
Ou seja, se houve uma variação de 1 semana a mais, em relação ao par ordenado (2,5), podemos concluir que para a grama alcançar 7 cm precisa de 3 semanas, ou seja, 21 dias.
Sendo assim, como ele quer o campo pronto no dia 11 de junho a grama deve ser plantada no dia 21 de maio, 21 dias antes.
Alternativa B






