Questão 137 – Logaritmo
Para realizar a viagem dos sonhos, uma pessoa precisava fazer um empréstimo no valor de R$ 5000,00. Para pagar as prestações, dispõe de, no máximo, R$ 400,00 mensais. Para esse valor de empréstimo, o valor da prestação (P) é calculado em função do número de prestações (n) segundo a fórmula
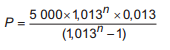
Se necessário, utilize 0,005 como aproximação para log 1,013; 2,602 como aproximação para log 400; 2,525 como aproximação para log 335.
De acordo com a fórmula dada, o menor número de parcelas cujos valores não comprometem o limite definido pela pessoa é
A) 12
B) 14
C) 15
D) 16
E) 17
Solução
A parcela P deve ser menor ou igual a 400, ou seja
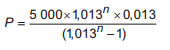
≤ 400
Resolvendo a equação acima temos
65 . 1,013n ≤ 400 . (1,013n – 1)
65 . 1,013n ≤ 400 . 1,013n – 400
400 ≤ 400 . 1,013n – 65 . 1,013n
400 ≤ 335 . 1,013n
400/335 ≤ 1,013n
Como temos uma variável no expoente vamos aplicar o log dos dois lados da equação
log (400/335) ≤ log 1,013n
log 400 – log 335 ≤ n . log 1,013
Pelos valores aproximamos dados no enunciado temos
2,602 – 2,525 ≤ n . 0,005
0,075/,005 ≤ n
15,4 ≤ n
O menor valor de inteiro de n possível é 16
Alternativa D
Veja a resolução com mais detalhes no vídeo abaixo!






