Questão 137 – Geometria Plana
O tampo de vidro de uma mesa quebrou-se e deverá ser substituído por outro que tenha a forma de círculo. O suporte de apoio da mesa tem o formato de um prisma reto, de base em forma de triângulo equilátero com lados medindo 30 cm.
Uma loja comercializa cinco tipos de tampos de vidro circulares com cortes já padronizados, cujos raios medem 18 cm, 26 cm, 30 cm, 35 cm e 60 cm. O proprietário da mesa deseja adquirir nessa loja o tampo de menor diâmetro que seja suficiente para cobrir a base superior do suporte da mesa.
Considere 1,7 como aproximação para √3.
O tampo a ser escolhido será aquele cujo raio, em centímetros, é igual a
A) 18
B) 26
C) 30
D) 35
E) 60
Solução
Para cobrir a base o trampo deve ter raio mínimo igual a r
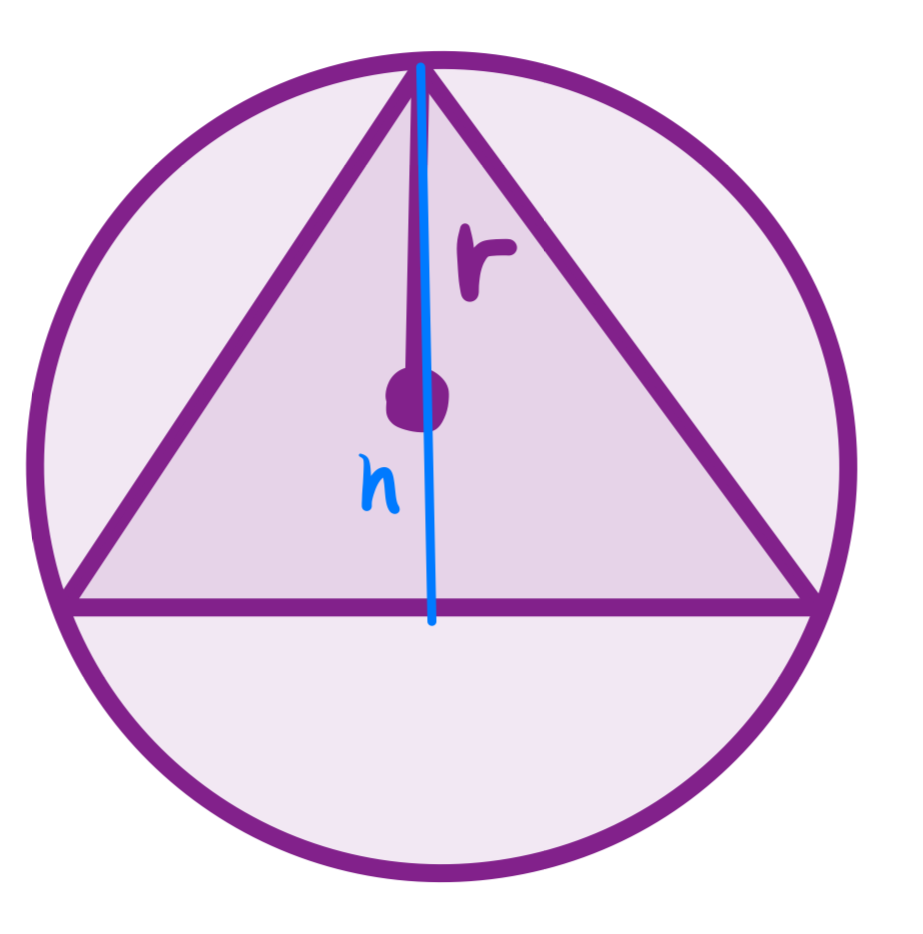
Para calcular r procuramos relembrar as propriedades de um triângulo inscrito em um círculo.
Sabemos que h, a altura do triângulo, está dividida em duas partes onde o raio equivale a (2/3) de h.
Para calcular h, sabemos que a altura do triângulo equilátero é l.√3/2, onde l equivale ao lado do triângulo. Sendo l=30, temos
h = 30.√3/2
h = 15 . 1,7
h = 25,5
Agora vamos calcular r
r = (2/3).h
r = 25,5 . 2/3
r = 17
O menor tampo possível é o tampo com raio 18cm.
Alternativa A






