No manejo sustentável de florestas, é preciso muitas vezes obter o volume da tora que pode ser obtida a partir de uma árvore. Para isso, existe um método prático, em que se mede a circunferência da árvore à altura do peito de um homem (1,30 m), conforme indicado na figura. A essa medida denomina-se “rodo” da árvore. O quadro a seguir indica a fórmula para se cubar, ou seja, obter o volume da tora em m³ a partir da medida do rodo e da altura da árvore.
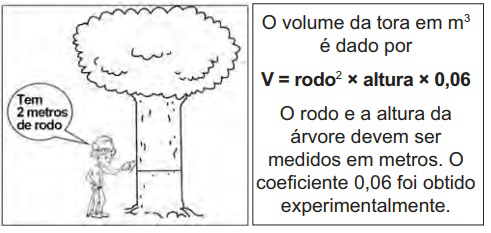
Um técnico em manejo florestal recebeu a missão de cubar, abater e transportar cinco toras de madeira, de duas espécies diferentes, sendo
• 3 toras da espécie I, com 3 m de rodo, 12 m de comprimento e densidade 0,77 toneladas/m³;
• 2 toras da espécie II, com 4 m de rodo, 10 m de comprimento e densidade 0,78 toneladas/m³.
Após realizar seus cálculos, o técnico solicitou que enviassem caminhões para transportar uma carga de, aproximadamente,
A) 29,9 toneladas.
B) 31,1 toneladas.
C) 32,4 toneladas.
D) 35,3 toneladas.
E) 41,8 toneladas.
Solução
Tomando o comprimento como a altura da árvore, vamos calcular o volume de acordo com a fórmula
Espécie 1:
Toras: 3
Rodo: 3 m
Altura: 12 m
Densidadede: 0,77
V = 3 . 9 . 12 . 0,06
V = 19,44 m3
Multiplicando o volume pela densidade descobrimos a massa aproximada dessas toras
M = 19,44 . 0,7 = 13,608 toneladas
Espécie 2:
Toras: 2
Rodo 4 m
Altura: 10 m
Densidade: 0,78
V = 2 . 16 . 10 . 0,06
V = 19,2 m3
Calculando a massa:
M = 19,2 . 0,78 = 14,976 toneladas
A carga total do caminhão é 13,608 + 14,976 = 28,584 toneladas
Alternativa A






