Questão 161 – Geometria Plana
Em canteiros de obras de construção civil é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo, foram indicadas por letras.
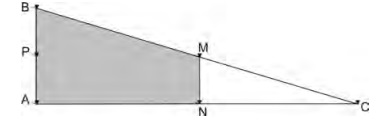
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto.
Nessas condições, a área a ser calçada corresponde
A) à mesma área do triângulo AMC.
B) à mesma área do triângulo BNC.
C) à metade da área formada pelo triângulo ABC.
D) ao dobro da área do triângulo MNC.
E) ao triplo da área do triângulo MNC.
Solução
Os pontos M, N e P dividem seus respectivos lados ao meio, com essa informação podemos concluir que
MC = BC/2
NC = AC/2
Ou seja a razão de semelhança entre o triângulo ABC para o MNC é k = 1/2.
Sabemos que a razão de semelhança entres as áreas é k2, ou seja
MNC/ABC = 1/4
Concluimos que a área do trîângulo ABC é 4 vezes a área do triângulo MNC.
Se a área do quadriláterio ABMN é a área do triângulo ABC – MNC, temos que a área do quadrilátero é 3 vezes a área do triângulo MNC.
Alternativa E
