Questão 136 – Matriz
Uma faculdade oferece dois cursos diferentes na área de Humanas. Para um aluno ingressar nesses cursos, o vestibular contém questões objetivas e uma redação, e a nota final do candidato é a soma dessas notas, utilizando o seguinte critério de pesos:
• questões objetivas: peso 1 para o curso I e peso 1 para o curso II;
• redação: peso 2 para o curso I e peso 3 para o curso II.
Um candidato que concorre aos dois cursos obteve nota X nas questões objetivas e nota Y na redação. Para analisar sua nota para o curso I e para o curso II, o candidato representa sua nota com um produto de matrizes A . B, em que a matriz A representa os pesos, e a matriz B contém as notas obtidas pelo candidato.
A matriz resultante A . B é uma matriz coluna, em que, na primeira linha, tem sua nota final para o curso I e, na segunda linha, tem sua nota final para o curso II. Nessas condições, qual representação algébrica gera o resultado final desse candidato nos dois cursos?
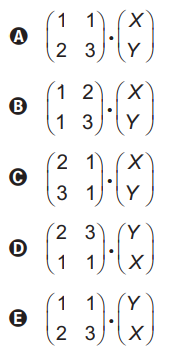
Resolução
Para multiplicar matrizes fazemos linha vezes coluna.
Na primeira matriz aparece os pesos e na segunda as notas.
temos que a primeira linha será para o curso 1 e a segunda para o curso 2.
Enquanto a primeira coluna será de provas objetivas e a segunda será para redação, como uma tabela!
Então a posição superior e a esquerda será o peso do curso 1 para a prova objetiva que é 1.
A posição superior e a direita será o peso do curso 1 para a redação que é 2.
Então a posição inferior e a esquerda será o peso do curso 2 para a prova objetiva que é 1.
A posição inferior e a direita será o peso do curso 2 para a redação que é 3.
Então será no formato da matriz da
Alternativa B
Assista a resolução com mais detalhe no vídeo abaixo!







top