Uma indústria recortou uma placa de metal no formato triangular ABC, conforme Figura 1, com lados 18, 14 e 12 cm.
Posteriormente, a peça triangular ABC foi dobrada, de tal maneira que o vértice B ficou sobre o segmento AC, e o segmento DE ficou paralelo ao lado AC, conforme figura 2.
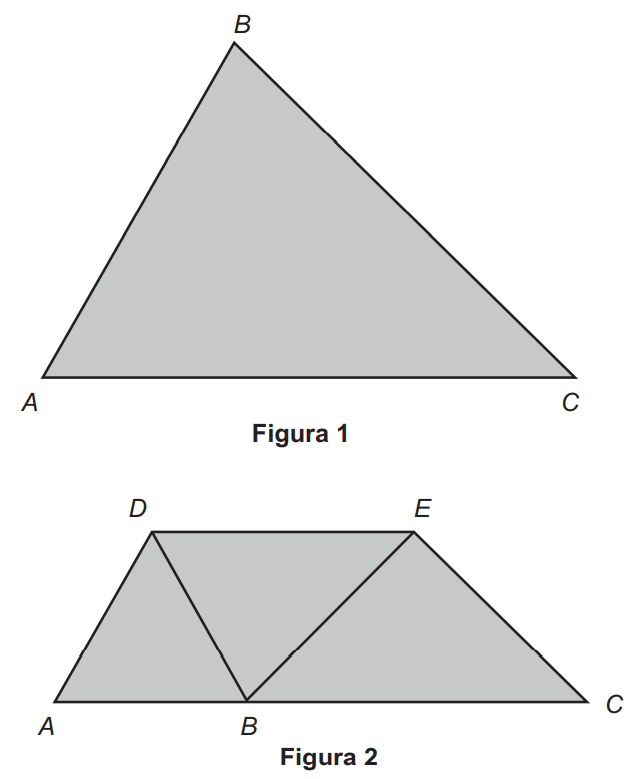
Sabe-se que, na Figura 1, o ângulo ACB é menor que o ângulo CAB e este é menor que o ângulo ABC, e que os cortes e dobraduras foram executados corretamente pelas máquinas.
Nessas condições, qual é o valor da soma dos comprimentos, em centímetro, dos segmentos DB, BE e EC?
A) 19
B) 20
C) 21
D) 23
E) 24
Resolução
Sabemos que BE + EC = BC
Sabemos também que ACB é menor que CAB e que CAB é menor que ABC, então temos
ACB<CAB<ABC
Com essa informação, pela propriedade de triângulos concluímos que os lados opostos a esses ângulos seguem essa mesma ordem, ou seja:
AB < BC < AC
Então AB = 12, BC = 14 e AC = 18
Então temos que BE + EC = 14
Falta descobrirmos então o valor de DB.
Quando fazemos a dobradura, enxergamos que dividimos a altura ao meio, ou seja, os triângulos formados Por DBE e ABC são semelhantes e são metade!
Consequentemente DE = AB/2
Então BE = 6
Somando com 14
14 + 6 = 20
Alternativa B
Assista à resolução com mais detalhes no vídeo abaixo!






