Questão 139 – Geometria Espacial
O dono de um salão de festas precisa decorar cinco pilastras verticais cilíndricas idênticas, cujo raio da base mede 10 cm. O objetivo é revestir integralmente essas pilastras com faixas de menor comprimento possível, de modo que cada uma tenha seis faixas de cor preta e cinco faixas de cor branca, conforme ilustrado na figura.
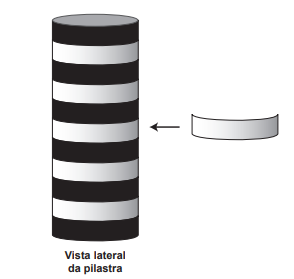
Ele orçou as faixas em cinco lojas que as comercializam na largura e nas cores desejadas, porém, em todas elas, só são vendidas peças inteiras. Os comprimentos e os respectivos preços das peças comercializadas por loja estão apresentados no quadro.
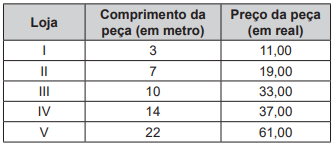
O dono do salão de festas decidiu efetuar a compra em uma única loja, optando por aquela em que a compra ficaria mais barata.
Utilize 3 como valor aproximado para π.
A loja na qual o dono do salão de festas deve comprar as peças necessárias para confeccionar as faixas é
A) I.
B) II.
C) III.
D) IV.
E) V.
Resolução
Vamos calcular o comprimento de cada faixa usando
2.π.r = 2.3.10 = 60 cm
Como serão necessárias 6 faixas pretas para cada pilastra e são 5 pilastras, serão necessários
60.6.5 = 1800 cm = 18 m de faixa preta
E como são 5 brancas por pilastra, serão necessários
60.5.5 = 1500 cm = 15 m de faixa branca
Para comprar na loja I, o dono gastará
6*11 + 5*11 =121 reais
Para comprar na loja II, o dono gastará
3*19 + 3*19 = 114 reais
Para comprar na loja III, o dono gastará
2*33 + 2*33 = 132 reais
Para comprar na loja IV, o dono gastará
2*37 + 2*37 = 148 reais
Para comprar na loja V, o dono gastará
1*61 + 1*61 = 122 reais
O lugar que será mais barato é na loja II
Alternativa B






