Questão 142 – Geometria Plana
As Artes Marciais Mistas, tradução do inglês: MMA – mixed martial arts, são realizadas num octógono regular. De acordo com a figura, em certo momento os dois lutadores estão respectivamente nas posições G e F, e o juiz está na posição I. O triângulo IGH é equilátero e GÎF é o ângulo formado pelas semirretas com origem na posição do juiz, respectivamente passando pelas posições de cada um dos lutadores.
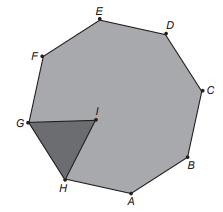
A medida do ângulo GÎF é
A) 120°
B) 75°
C) 67,5°
D) 60°
E) 52,5°
Resolução
Se IGH é equilátero, então
GH = GI
Se temos um octógono regular, posso afirmar que
GH = FG
Consequentemente
FG = GI
Ou seja, o triângulo GIF é isósceles com base em FI, portanto os ângulos GIF e GFI são iguais.
Basta descobrir o valor do ângulo IGF para descobrir o valor dos outros dois ângulos.
Podemos calcular o valor do ângulo FGH usando a fórmula de ângulos internos de um polígono
(n -2)180/n
Como é um octógono, n=8
FGH = (8-2)180/8 = 135
Se o triângulo GIH é equilátero, todos os ângulos são 60, então
IGH = 60
Sendo
IGF = FGH – IGH
Temos que
IGF = 135 – 60
IGF = 75
Sabemos que a soma dos ângulos internos de um triângulo é 180, então
IGF + GIF + GFI = 180
Se
GIF = GFI
como falamos anteriormente, então
IGF + 2.GIF = 180
Substituindo o valor de IGF
75 + 2.GIF = 180
2.GIF = 105
GIF = 52,5
Alternativa E






