Um gesseiro que trabalhava na reforma de uma casa lidava com placas de gesso com formato de pentágono regular quando percebeu que uma peça estava quebrada, faltando uma parte triangular, conforme mostra a figura.
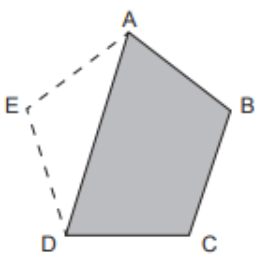
Para recompor a peça, ele precisou refazer a parte triangular que faltava e, para isso, anotou as medidas dos ângulos x = EAD, y = EDA e z = AED do triângulo ADE. As medidas x, y e z, em graus, desses ângulos são, respectivamente,
A) 18, 18 e 108.
B) 24, 48 e 108.
C) 36, 36 e 108.
D) 54, 54 e 72.
E) 60, 60 e 60.
Solução
O ângulo interno de um pentágono é calculado pela fórmula, sendo n o numero de lados
180(n-2)/n = 180(5-2)/5 = 180.3/5 = 540/5 = 108
Se os ângulos internos são 108, z = 108
Sabemos também que por ser um pentágono regular os lados EA e ED são iguais, consequentemente os seus ângulos opostos também.
Concluímos que o triângulo EAD é isósceles e y = z, então, a soma dos ângulos internos é 180
180 = 108 + y + z
180 = 108 + y + y
180 = 108 + 2y
2y = 180 – 108
2y = 72
y = 36
Alternativa C






