Três amostras de minérios de ferro de regiões distintas foram analisadas e os resultados, com valores aproximados, estão na tabela:
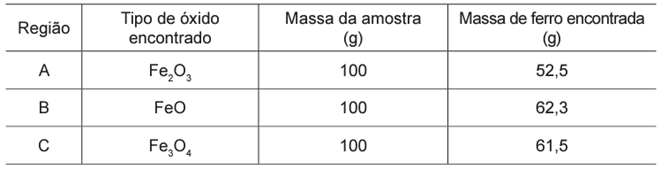
Considerando que as impurezas são inertes aos compostos envolvidos, as reações de redução do minério de ferro com carvão, de formas simplificadas, são:
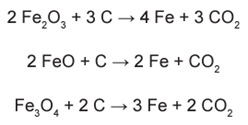
Dados: Massas molares (g/mol) C = 12; O = 16; Fe = 56; FeO = 72; Fe2O3 = 160; Fe3O4 = 232.
Os minérios que apresentam, respectivamente, a maior pureza e o menor consumo de carvão por tonelada de ferro produzido são os das regiões:
A) A com 75% e C com 143 kg.
B) B com 80% e A com 161 kg.
C) C com 85% e B com 107 kg.
D) A com 90% e B com 200 kg.
E) B com 95% e A com 161 kg.
Solução
Primeiramente, precisamos calcular a pureza de cada amostra. Para isso, vamos utilizar a massa total das amostras, que é de 100 g, e a massa de ferro encontrada em cada uma delas, conforme registrado na tabela. A porcentagem de pureza de cada óxido será determinada pela relação entre a massa do ferro encontrado e a massa total da amostra.
AMOSTRA DA REGIÃO A: 2 mol de Fe2O3, formam 4 mol de Fe. Se a massa de Fe obtida através do óxido em questão foi de 52,5 g, podemos descobrir a quantidade de Fe2O3 que reagiu:
2 Fe2O3 + 3 C → 4 Fe + 3 CO2
Fe2O3 Fe
2 160 g ———– 4 56 g
x ——————— 52,5 g
x = 75 g de Fe2O3
Para produzir 52,5 g de Fe, foram necessários 75 g de Fe2O3. Se a amostra tem massa total de 100 g, a pureza é de 75%. Os outros 25% (25 g) não correspondem ao Fe2O3.
AMOSTRA DA REGIÃO B: 2 mol de FeO, formam 2 mol de Fe. Se a massa de Fe obtida através do óxido em questão foi de 62,3 g, podemos descobrir a quantidade de FeO que reagiu:
2 FeO + C → 2 Fe + CO2
FeO Fe
2 72 g ———– 2 56 g
y ——————— 62,3 g
y = 80 g de FeO
Para produzir 62,3 g de Fe, foram necessários 80 g de FeO. Se a amostra tem massa total de 100 g, a pureza é de 80%. Os outros 20% (20 g) não correspondem ao FeO.
AMOSTRA DA REGIÃO C: 1 mol de Fe3O4, forma 3 mol de Fe. Se a massa de Fe obtida através do óxido em questão foi de 61,5 g, podemos descobrir a quantidade de Fe3O4 que reagiu:
Fe3O4 + 2 C → 3 Fe + 2 CO2
Fe3O4 Fe
232 g ———– 3 56 g
z ——————— 61,5 g
z = 85 g de Fe3O4
Para produzir 61,5 g de Fe, foram necessários 85 g de FeO. Se a amostra tem massa total de 100 g, a pureza é de 85%. Os outros 15% (15 g) não correspondem ao Fe3O4.
O segundo passo consiste em determinar a quantidade de carvão necessária para produzir uma tonelada de ferro em diferentes reações químicas. Vamos calcular o consumo de carvão para cada reação usando as equações químicas e outros dados fornecidos:
REGIÃO A. Reação: 2 Fe2O3 + 3 C → 4 Fe + 3 CO2
– Dados: 3 mol de carbono (carvão) formam 4 mol de Fe.
– Para 1000 kg de Fe, a quantidade de carvão necessária é dada por:
C Fe
3 12 g ———– 4 56 g
A ——————- 1000 kg
A = 160,7 kg de carvão
REGIÃO B. Reação: 2 FeO + C → 2 Fe + CO2
– Dados: 1 mol de C forma 2 mol de Fe.
– Para 1000 kg de Fe, a quantidade de carvão necessária é dada por:
C Fe
12 g —————– 2 56 g
B ——————- 1000 kg
B = 107,1 kg de carvão
REGIÃO C. Reação: Fe3O4 + 2 C → 3 Fe + 2 CO2
– Dados: 2 mol de C formam 3 mol de Fe.
– Para 1000 kg de Fe, a quantidade de carvão necessária é dada por:
C Fe
2 12 g —————– 3 56 g
B ——————- 1000 kg
B = 143,8 kg de carvão
Após a análise dos cálculos, observamos que a pureza do carvão é mais alta no minério da região C, com 85%. Já a reação B é a que apresenta o menor consumo de carvão para produzir uma tonelada de ferro
Alternativa C






