Para fazer um pião, brinquedo muito apreciado pelas crianças, um artesão utilizará o torno mecânico para trabalhar num pedaço de madeira em formato de cilindro reto, cujas medidas do diâmetro e da altura estão ilustradas na Figura 1. A parte de cima desse pião será uma semiesfera, e a parte de baixo, um cone com altura 4 cm, conforme Figura 2. O vértice do cone deverá coincidir com o centro da base do cilindro.
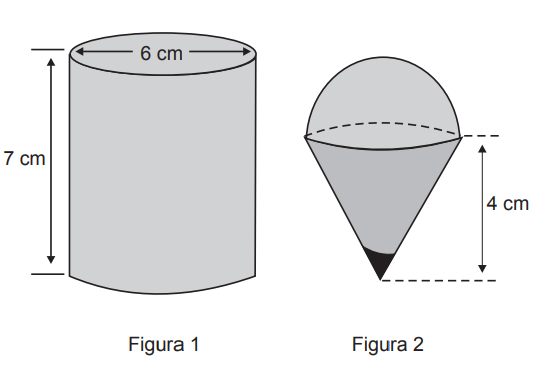
O artesão deseja fazer um pião com a maior altura que esse pedaço de madeira possa proporcionar e de modo a minimizar a quantidade de madeira a ser descartada.
Dados:
O volume de uma esfera de raio r é 4·π·r³/3;
O volume do cilindro de altura h e área da base S é S·h;
O volume do cone de altura h e área da base S é 1/3 ·S·h;
Por simplicidade, aproxime π para 3.
A quantidade de madeira descartada, em centímetros cúbicos, é
A) 45.
B) 48.
C) 72.
D) 90.
E) 99.
Solução
Como sei que o raio da semiesfera é a distância entre a base da pirâmide e a extremidade mais alta da semiesfera, podemos dizer que o raio da semiesfera r será
r = 7 – 4 = 3 cm
Como os raios devem coincidir o raio do cone também será r = 3 cm, consequentemente para descobrir quanto de madeira foi deduzido do formato cônico basta subtrairmos o volume de um cone de base de raio r = 3 cm de um cilindro de mesma base já que o diâmetro do cilindro é 6 cm. Ambos tem altura 4 cm
Então teremos
π·r²·h – π·r²·h/3
Que substituindo os valores temos
π.3².4 – π.3².4/3 = 36π – 12π = 24π = 72 cm³
Agora vamos calcular a quantidade de madeira perdida na parte da semiesfera subtraindo de um cilindro de altura de 3 cm e raio 3 cm.
π·r²·h – (4·π·r³/3)/2 = π.3².3 – (4.π.3³/3)/2 = 27π – 18π = 27 cm³
O volume descartado foi
72 + 27 = 99 cm³
Alternativa E






