A Regra de Três Composta é uma ferramenta matemática utilizada para resolver problemas que envolvem mais de duas grandezas relacionadas. Ela é uma extensão da Regra de Três Simples e é fundamental para lidar com situações do cotidiano e questões de concursos que exigem a análise de múltiplas variáveis.
O que é a Regra de Três Composta?
A Regra de Três Composta é um método que permite encontrar um valor desconhecido em problemas que envolvem três ou mais grandezas que se relacionam de forma proporcional, seja diretamente, seja inversamente . Ela é amplamente aplicada em contextos como:
- Cálculos de produção
- Planejamento de obras
- Conversões de unidades
- Problemas de escalas
Diferença entre Regra de Três Simples e Composta
Enquanto a Regra de Três Simples envolve apenas duas grandezas, a Regra de Três Composta lida com três ou mais. A principal diferença está na complexidade e na quantidade de variáveis envolvidas:
- Regra de Três Simples: Relaciona duas grandezas, sendo uma delas a incógnita.
- Regra de Três Composta: Relaciona três ou mais grandezas, sendo uma delas a incógnita, e exige a análise das relações de proporcionalidade entre elas .
Passo a Passo para Resolver Regra de Três Composta
- Identificar as Grandezas Envolvidas: Liste todas as grandezas presentes no problema e determine qual delas é a incógnita.
- Construir uma Tabela: Organize os dados em uma tabela, colocando as grandezas em colunas e os valores correspondentes em linhas.
- Analisar as Relações de Proporcionalidade: Determine se cada grandeza é diretamente ou inversamente proporcional à grandeza que contém a incógnita.
- Montar a Equação: Com base nas relações identificadas, monte uma equação que permita encontrar o valor desconhecido.
- Resolver a Equação: Efetue os cálculos necessários para encontrar o valor da incógnita.
Exemplos Práticos
Problema: Uma construtora foi contratada para realizar a reforma de todas as escolas de um município. Sabe-se que 4 pintores levam 8 dias para pintar 6 escolas. Quantos dias serão necessários para que 8 pintores pintem 18 escolas?
Solução:
- Grandezas: Pintores, Dias, Escolas.
- Tabela:
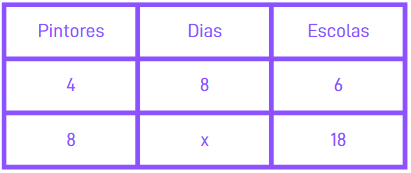
3. Análise de Proporcionalidade:
- Dias e Pintores: Mais dias, menos pintores serão necessários → Inversamente proporcional.
- Dias e Escolas: Mais dias, mais escolas → Diretamente proporcional.
Assim colocamos as setas sempre tendo a grandeza com a variável:
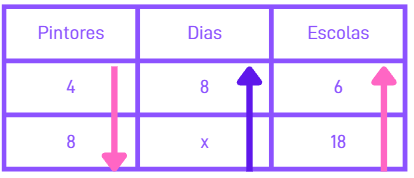
4. Montagem da Equação:
8/x = (6/18) . (8/4)
Resolvendo:
8/x = (1/3) . 2
8/x = 2/3
8.3/2 = x
x = 12
Resposta: 12 dias.
A Regra de Três Composta é uma ferramenta essencial para resolver problemas que envolvem múltiplas grandezas relacionadas. Ao compreender as relações de proporcionalidade e seguir um processo organizado, é possível encontrar soluções precisas para situações complexas do cotidiano e de contextos acadêmicos.






