Um estudante leu em um site da internet que os povos antigos determinavam a duração das estações do ano observando a variação do tamanho da sombra de uma haste vertical projetada no solo. Isso ocorria porque, se registrarmos o tamanho da menor sombra ao longo de um dia (ao meio-dia solar), esse valor varia ao longo do ano, o que permitiu aos antigos usar esse instrumento rudimentar como um calendário solar primitivo. O estudante também leu que, ao longo de um ano (sempre ao meio-dia solar): (I) a sombra é máxima no solstício de inverno; e (II) a sombra é mínima no solstício de verão.
O estudante, que morava em Macapá (na Linha do Equador), ficou intrigado com essas afirmações e resolveu verificar se elas eram verdadeiras em diferentes regiões do mundo. Contactou seus amigos virtuais em Salvador (Região Tropical) e Porto Alegre (Região Temperada) e pediu que eles registrassem o tamanho da menor sombra de uma haste vertical padronizada, ao longo do dia, durante um ano. Os resultados encontrados estão mostrados esquematicamente no gráfico (SV: Solstício de Verão; SI: Solstício de Inverno; E: Equinócio):
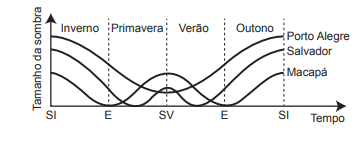
Qual(is) cidade(s) indicada(s) no texto e no gráfico contradiz(em) a afirmação II?
A) Salvador.
B) Porto Alegre.
C) Macapá e Salvador.
D) Macapá e Porto Alegre.
E) Porto Alegre e Salvador.
Solução
A afirmação (II) é a seguinte: “a sombra é mínima no Solstício de Verão” (SV). O período SV encontra-se no meio do gráfico. Para que a sombra seja mínima, a altura da curva em SV deve ser a mais baixa possível em comparação aos outros períodos.
A curva de Porto Alegre possui seu mínimo em SV, não contradizendo a afirmação (II).
As curvas de Salvador e Macapá não têm seus mínimos em SV, pelo contrário, apresentam um pico nessa região. Os mínimos do Macapá se encontram nos Equinócios (E), e os mínimos de Salvador se encontram na Primavera e no Verão, o que contradiz a afirmação (II).
Alternativa C






