Questão 136 – Geometria Espacial
Em regiões agrícolas, é comum a presença de silos para armazenamento e secagem da produção de grãos, no formato de um cilindro reto, sobreposto por um cone, e dimensões indicadas na figura. O silo fica cheio e o transporte dos grãos é feito em caminhões de carga cuja capacidade é de 20 m³. Uma região possui um silo cheio e apenas um caminhão para transportar os grãos para a usina de beneficiamento.
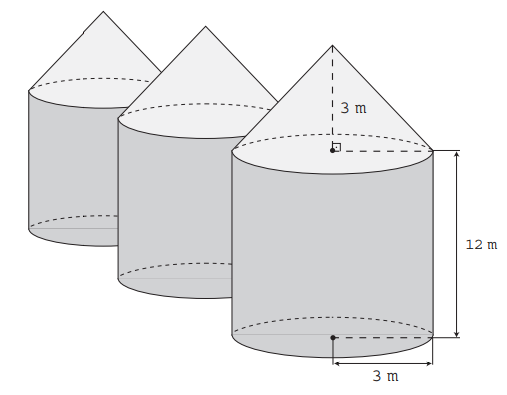
Utilize 3 como aproximação para π.
O número mínimo de viagens que o caminhão precisará fazer para transportar todo o volume de grãos armazenados no silo é
A) 6
B) 16
C) 17
D) 18
E) 21
Solução
Vamos calcular o volume do silo que é a junção de um cilindro com um cone de bases circular de raio 3 m.
Para calcular o volume do cone basta fazermos a área da base vezes a altura dividida por 3.
V = A.h/3
A área da base circular se dá por πr2, então
A = π32 = 9π = 27
Então o volume do cone é
V = 27.3/3 = 27 m3
Enquanto o volume do cilindro é área da base vezes sua altura
V = A.H
V = 27 . 12 = 324 m3
Somando os volumes temos
27 + 324 = 351 m3
Se cada caminhão transporta 20 m3 basta dividir
351/20 = 17,55
Serão necessárias 18 viagens.
Alternativa D






