Questão 136 – Geometria Plana
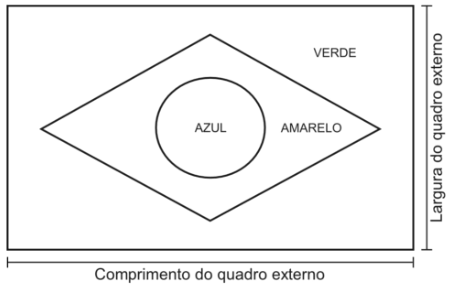
A fabricação da Bandeira Nacional deve obedecer ao descrito na Lei n. 5.700, de 1º de setembro de 1971, que trata dos Símbolos Nacionais. No artigo que se refere às dimensões da Bandeira, observa-se:
“Para cálculos das dimensões, será tomada por base a largura, dividindo-a em 14 (quatorze) partes iguais, sendo que cada uma das partes será considerada uma medida ou um módulo (M). Os demais requisitos dimensionais seguem o critério abaixo:
I. Comprimento será de vinte módulos (20 M);
II. A distância dos vértices do losango amarelo ao quadro externo será de um módulo e sete décimos (1,7 M);
III. O raio do círculo azul no meio do losango amarelo será de três módulos e meio (3,5 M).”
BRASIL, Lei n. 5.700, de 1° de setembro de 1971. Disponível em: www.planalto.gov.br. Acesso em: 15 set. 2015.
A figura indica as cores da bandeira do Brasil e localiza o quadro externo a que se refere a Lei n. 5.700.
Um torcedor, preparando-se para a Copa do Mundo e dispondo de cortes de tecidos verde (180 cm x 150 cm) e amarelo (o quanto baste), deseja confeccionar a maior Bandeira Nacional possível a partir das medidas do tecido verde.
Qual a medida, em centímetro, do lado do menor quadrado de tecido azul que deverá ser comprado para confecção do círculo da bandeira desejada?
A) 27
B) 32
C) 53
D) 63
E) 90
Solução
O tecido azul terá lado do tamanho do diâmetro para que seja possível cortar um círculo como ilustra a imagem

Para descobrir a dimensão correspondente ao raio do círculo precisamos calcular o valor do módulo M.
As dimensões do tecido verde usado na bandeira dependem do tanto de pano disposto, sendo 180cm x 150cm, se a proporção em módulo é 20M x 14M, temos duas opções para M.
180/20 = 9 cm
150/14 ≈10,7 cm
M deve ser 9, pois se for 10,7 o torcedor não terá tecido suficientes para as duas dimensões.
Se M = 9 o raio do círculo é
R = 3,5.M = 3,5 . 9 = 31,5 cm
Sendo o diâmetro o dobro do raio, a medida do lado do quadrado de tecido azul é 2 . 31,5 = 63 cm
Alternativa D
Veja a resolução com mais detalhes no vídeo abaixo!






