Questão 137 – Matemática Básica (Matemática Financeira)
Um contrato de empréstimo prevê que quando uma parcela é paga de forma antecipada, conceder-se-á uma redução de juros de acordo com o período de antecipação. Nesse caso, paga-se o valor presente, que é o valor, naquele momento, de uma quantia que deveria ser paga em uma data futura. Um valor presente P submetido a juros compostos com taxa i, por um período de tempo n, produz um valor futuro V determinado pela fórmula:
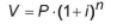
Em um contrato de empréstimo com sessenta parcelas fixas mensais, de R$820,00, a uma taxa de juros de 1,32% ao mês, junto com a trigésima parcela será paga antecipadamente uma outra parcela, desde que o desconto seja superior a 25% do valor da parcela.
Utilize 0,2877 como aproximação para In(4/3) e 0,0131 como aproximação para In(1,0132).
A primeira das parcelas que poderá ser antecipada junto com a 30ª é a
A) 56ª
B) 55ª
C) 52ª
D) 51ª
E) 45ª
Solução
O juros é de 1,32%, então i = 0,0132
Calculando
820/(1,0132)n = 0,75.820
descobrimos qual a parcela n terá o desconto de 25%.
Lembrando que 0,75 = 3/4, temos
820/(1,0132)n = 820. 3/4
1/(1,0132)n = 3/4
(1,0132)n = 4/3
ln(1,0132)n = ln(4/3)
n . ln(1,0132) = ln(4/3)
Substituindo os valores dados no enunciado para ln(1,0132) e ln(4/3)
n . 0,0131 = 0,2877
n = 0,2877/0,0131
n = 21,9…
Além das 30 parcelas, serão necessárias mais 22. Resultando em um total de 52 parcelas.
Alternativa C
Veja a resolução com mais detalhes no vídeo abaixo






