Questão 138 – Função Exponencial
A população mundial está ficando mais velha, os índices de natalidade diminuíram e a expectativa de vida aumentou. No gráfico seguinte, são apresentados dados obtidos por pesquisa realizada pela Organização das Nações Unidas (ONU), a respeito da quantidade de pessoas com 60 anos ou mais em todo o mundo. Os números da coluna da direita representam as faixas percentuais. Por exemplo, em 1950 havia 95 milhões de pessoas com 60 anos ou mais nos países desenvolvidos, número entre 10% e 15% da população total nos países desenvolvidos.
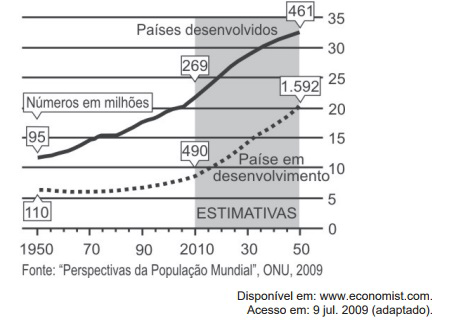
Suponha que o modelo exponencial y = 363e0,03x, em que x = 0 corresponde ao ano 2000, x = 1 corresponde ao ano 2001, e assim sucessivamente, e que y é a população em milhões de habitantes no ano x, seja usado para estimar essa população com 60 anos ou mais de idade nos países em desenvolvimento entre 2010 e 2050.
Desse modo, considerando e0,3 = 1,35, estima-se que a população com 60 anos ou mais estará, em 2030, entre
A) 490 e 510 milhões.
B) 550 e 620 milhões.
C) 780 e 800 milhões.
D) 810 e 860 milhões.
E) 870 e 910 milhões.
Solução
Queremos o valor no ano de 2030, ou seja, x = 30, usando a fórmula y = 363e0,03x, temos
y = 363e0,03.30
y = 363e0,9
y = 363(e0,3)3
Sabemos que e0,3 = 1,35
y = 365.1,353
y = 898 milhões
Alternativa E






