Questão 138 – Geometria Analítica
Um jogo pedagógico utiliza-se de uma interface algébrico-geométrica do seguinte modo: os alunos devem eliminar os pontos do plano cartesiano dando “tiros”, seguindo trajetórias que devem passar pelos pontos escolhidos. Para dar os tiros, o aluno deve escrever em uma janela do programa a equação cartesiana de uma reta ou de uma circunferência que passa pelos pontos e pela origem do sistema de coordenadas. Se o tiro for dado por meio da equação da circunferência, cada ponto diferente da origem que for atingido vale 2 pontos. Se o tiro for dado por meio da equação de uma reta, cada ponto diferente da origem que for atingido vale 1 ponto. Em uma situação de jogo, ainda restam os seguintes pontos para serem eliminados: A(0 ; 4), 6(4 ; 4), C(4 ; 0), D(2 ; 2) e E(0; 2).
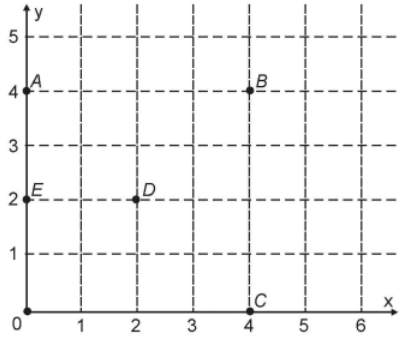
Passando pelo ponto A, qual equação forneceria a maior pontuação?
A) x = 0
B) y = 0
C) x² + y² =16
D) x² + (y-2)² = 4
E) (x -2 )² + ( y – 2 )² = 8
Solução
Vamos observar cada alternativa
A) x = 0, passa pelo ponto A e E.
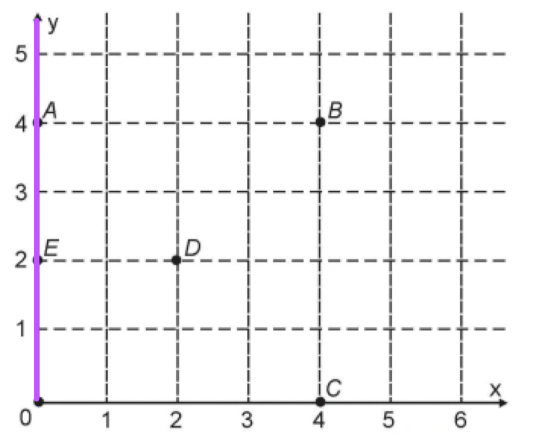
B) y = 0, passa pelo ponto C.
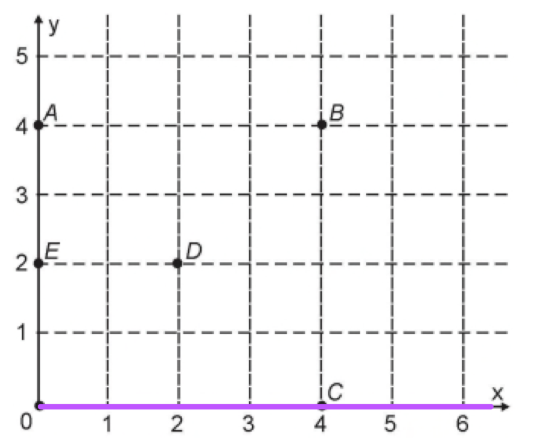
C) x² + y² =16, raio 4, passa pelos pontos A e C.
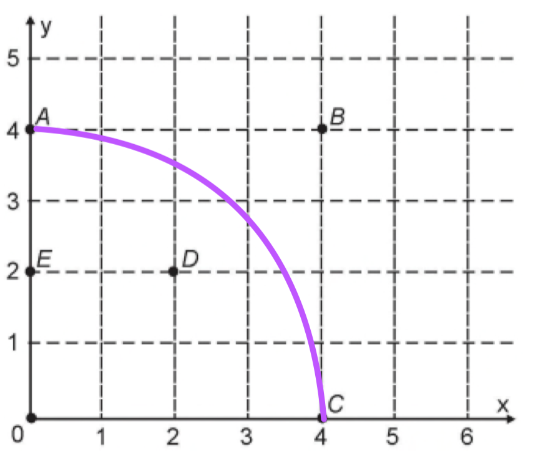
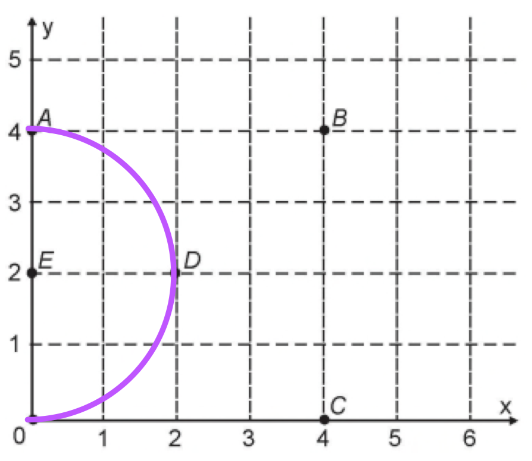
D) x² + (y-2)² = 4, raio 2, passa pelos pontos A e D.
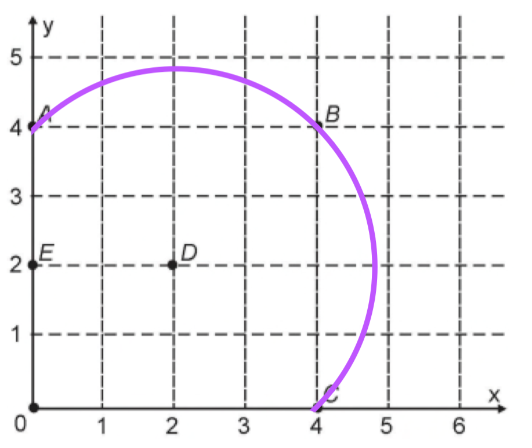
E) (x -2 )² + ( y – 2 )² = 8, raio igual a 2√2, passa pelos pontos A, B e C.
A equação que passa por mais pontos é a equação da
Alternativa E
Veja a resolução com mais detalhes no vídeo abaixo






