Questão 141 – Geometria Plana
Em um sistema de dutos, três canos iguais, de raio externo 30 cm, são soldados entre si e colocados dentro de um cano de raio maior, de medida R. Para posteriormente ter fácil manutenção, é necessário haver uma distância de 10 cm entre os canos soldados e o cano de raio maior. Essa distância é garantida por um espaçador de metal, conforme a figura:
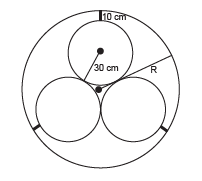
Utilize 1,7 como aproximação para √3
O valor de R, em centímetros, é igual a
A) 64,0
B) 65,5
C) 74,0
D) 81,0
E) 91,0
Solução
Formando um triângulo equilátero com os raios das pequenas circunferência temos que
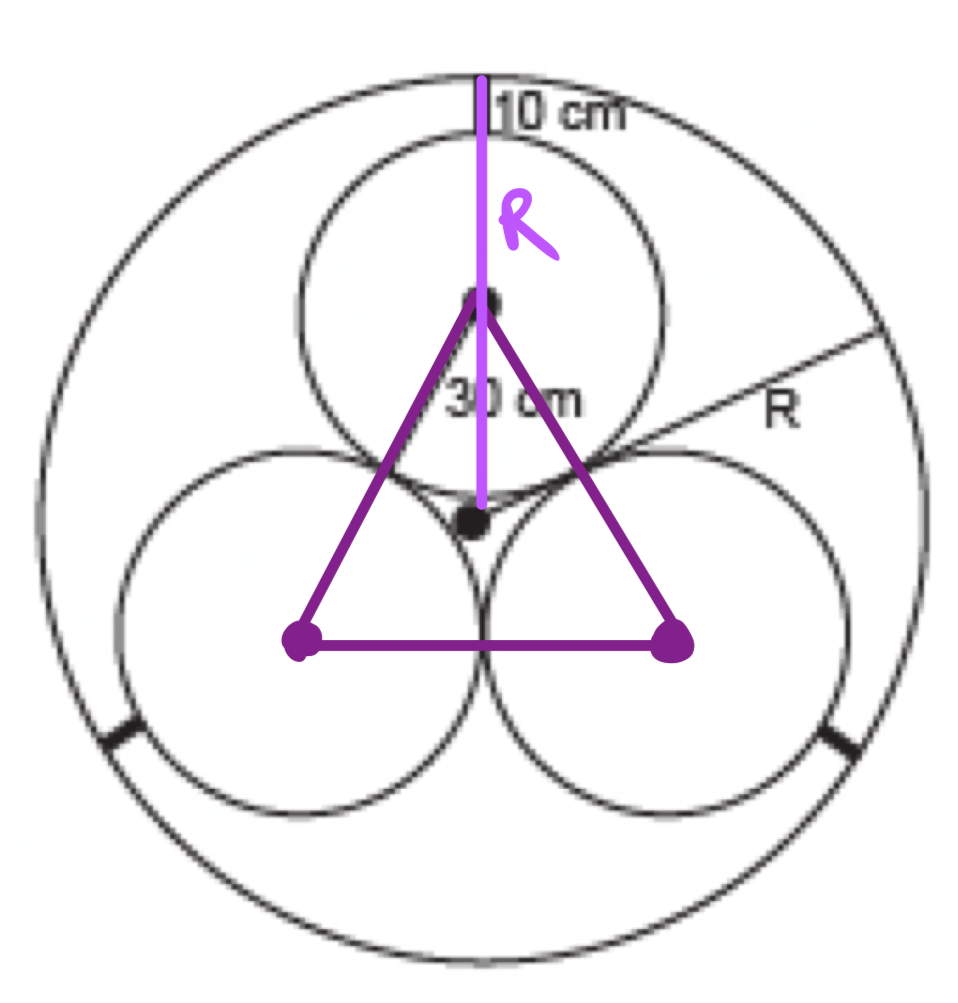
O raio R é10 cm mais o raio da pequena circunferência que é 30 cm, mais 2/3 da altura do triângulo equilátero.
Para calcular a altura h do triângulo basta usar a fórmula
h = l√3/2
O lado l é 2 vezes o raio, então h é
h = 60.√3/2
h = 30.1,7
h = 51 cm
Portanto 2/3 de 51 é
51.2/3 = 34
Somando tudo temos
10 + 30 + 34 = 74 cm
Alternativa C






