Questão 141 – Análise Combinatória
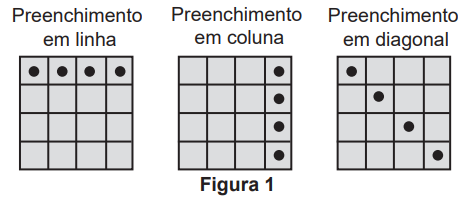
Em um jogo de bingo, as cartelas contém 16 quadrículas dispostas em linhas e colunas. Cada quadrícula tem impresso um número, dentre os inteiros de 1 a 50, sem repetição de número. Na primeira rodada, um número é sorteado, aleatoriamente, dentre os 50 possíveis. Em todas as rodadas, o número sorteado é descartado e não participa dos sorteios das rodadas seguintes. Caso o jogador tenha em sua cartela o número sorteado, ele o assinala na cartela. Ganha o jogador que primeiro conseguir preencher quatro quadrículas que formam uma linha, uma coluna ou uma diagonal, conforme os tipos de situações ilustradas na Figura 1.
O jogo inicia e, nas quatro primeiras rodadas, foram sorteados os seguintes números: 03, 27, 07 e 48. Ao final da quarta rodada, somente Pedro possuía uma cartela que continha esses quatro números sorteados, sendo que todos os demais jogadores conseguiram assinalar, no máximo, um desses números em suas cartelas. Observe na Figura 2 o cartão de Pedro após as quatro primeiras rodadas.
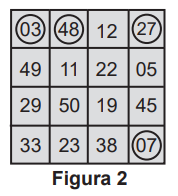
A probabilidade de Pedro ganhar o jogo em uma das duas próximas rodadas é
A) 1/46 + 1/45
B) 1/46 + 2/(46.45)
C) 1/46 + 8/(46.45)
D) 1/46 + 43/(46.45)
E) 1/46 + 49/(46.45)
Solução
Para Pedro ganhar direto na primeira rodada, só pode acontecer 1 coisa: sortear o número 12, na qual a chance é 1 em 46, ou seja, 1/46
Para Pedro ganhar na segunda rodada, ele pode fechar a quarta coluna, a diagonal ou tirar o número 12 na segunda rodada. Fechando a 4ª coluna, precisamos que tenham sido sorteados dois números específicos: na primeira rodada um deles, na segunda rodada o outro, ou seja
2/46 . 1/45
Fechando a diagonal:
Mesma situação que a anterior
2/46 . 1/45
Número 12 ser sorteado na 2ª rodada:
Na primeira rodada pode ter sido qualquer um menos o 12, e na segunda so pode ter sido sortada o 12, então temos:
45/46 . 1/45
Somando todas as frações temos:
1/46 + (2+2+45)/(46.45)
= 1/46 + 49/(46.45)
Alternativa E
Veja a resolução com mais detalhes no vídeo abaixo!






