Com base na Lei Universal da Gravitação, proposta por Isaac Newton, o peso de um objeto na superfície de um planeta aproximadamente esférico é diretamente proporcional à massa do planeta e inversamente proporcional ao quadrado do raio desse planeta. A massa do planeta Mercúrio é, aproximadamente, 1/20 da massa da Terra e seu raio é, aproximadamente, 2/5 do raio da Terra. Considere um objeto que, na superfície da Terra, tenha peso P. O peso desse objeto na superfície de Mercúrio será igual a
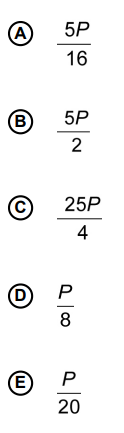
Resolução
O enunciado da questão informa que o peso (P) é diretamente proporcional a massa e inversamente o quadrado do raio, assim temos:
P = M/R²
Assim, sabemos que a massa do planeta Mercúrio é 1/20 da massa da Terra:
Mm= 1/20 *Mt
E o raio de Mercúrio é 2 / 5 do raio da Terra:
Rm = 2 / 5 *Rt
Substituindo temos:
P = Mt/20
———-
( 2/ 5*Rt)²
P = Mt/20
———
4/25*Rt²
P = Mt /20 * 25/4*Rt²
P = 25Mt/20*4*Rt²
Simplificando o 20 e o 25 por 5 temos:
P = 5Mt /4*4*Rt²
P = 5Mt /16*Rt²
Mt/Rt² correspondem ao P, assim podemos cancelar, ficando com:
5/16P
Alternativa A






