Questão 143 – Função de 2o grau
No desenvolvimento de um novo remédio, pesquisadores monitoram a quantidade Q de uma substância circulando na corrente sanguínea de um paciente, ao longo do tempo t. Esses pesquisadores controlam o processo, observando que Q é uma função quadrática de t. Os dados coletados nas duas primeiras horas foram:
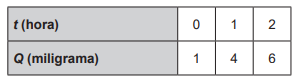
Para decidir se devem interromper o processo, evitando riscos ao paciente, os pesquisadores querem saber, antecipadamente, a quantidade da substância que estará circulando na corrente sanguínea desse paciente após uma hora do último dado coletado. Nas condições expostas, essa quantidade (em miligrama) será igual a
A) 4.
B) 7.
C) 8.
D) 9.
E) 10.
Resolução
Uma função de 2o grau é escrito no formato
y = ax² + bx + c
No nosso caso Q é y e t é x, sabemos que
quanto t = 0, Q = 1, ou seja
1 = 0a +0b + c
c = 1
Agora que sabemos que c é 1 podemos fazer o mesmo passo a passo criando um sistema de equações para descobrir a e b
quando t = 1, Q = 4
4 = 1a + 1b + 1
a + b = 3
quando t = 2, Q = 6
6 = 4a + 2b + 1
4a + 2b = 5
O sistema de equações
a + b = 3
4a + 2b = 5
Fazendo por adição
Multiplicando a primeira equação por -2 e somando a segunda equação temos
4a -2a + 2b – 2b = 5 – 6
2a = -1
a = -1/2
Substituindo esse valor na equação temos
-1/2 + b = 3
b = 7/2
Então a equação é no formato
y = -x²/2 + 7x/2 + 1
Uma hora depois da última informação coletada é com t = 3
Q = -3²/2 + 7.3/2 + 1
Q = -9/2 + 21/2 + 1
Q = 12/2 + 1
Q = 6 + 1
Q = 7
Alternativa B






