Questão 144 – Geometria Plana
Os alunos do curso de matemática de uma universidade desejam fazer uma placa de formatura, no formato de um triângulo equilátero, em que os seus nomes aparecerão dentro de uma região quadrada, inscrita na placa, conforme a figura.
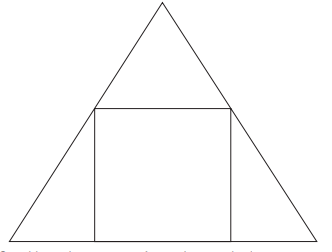
Considerando que a área do quadrado, em que aparecerão os nomes dos formandos, mede 1 m2 , qual é aproximadamente a medida, em metro, de cada lado do triângulo que representa a placa? (Utilize 1,7 como valor aproximado para √3 ).
A) 1,6
B) 2,1
C) 2,4
D) 3,7
E) 6,4
Resolução
Observemos que a base do triângulo formado no topo da figura é um dos lados do quadrado, que por ter área 1 m², tem lado L
L² = 1
L = 1
A reta que forma essa base do triângulo superior é paralela a base do triângulo maior, ou seja, o triângulo superior é semelhante ao maior!
Concluindo que é um triângulo equilátero também!
Se o triângulo no topo tem lados iguais a 1 basta agora calcular a hipotenusa do triângulo retângulo formado embaixo.
Sabendo que o ângulo da base é 60 e que o cateto oposto a esse angulo é o lado do quadrado que mede 1, podemos calcular a hipotenusa com o sen60.
Sendo a hipotenusa x, podemos afirmar que
sen 60 = 1/x
e sabemos também que
sen 60 = √3/2
igualando essas duas frações temos
1/x = √3/2
resolvendo multiplicando cruzado
√3x = 2
x = 2/√3
x = 2/1,7
x = 1,17
Somando o lado do triângulo equilátero de lado 1 mais x, temos
1 + 1,17 = 2,17
Alternativa B
Assista a resolução com mais detalhes no vídeo abaixo!






