Um fazendeiro pretende construir um galinheiro ocupando uma região plana de formato retangular, com lados de comprimentos L metro e C metro. Os lados serão cercados por telas de tipos diferentes. Nos lados de comprimento L metro, será utilizada uma tela cujo metro linear custa R$ 20,00, enquanto, nos outros dois lados, uma que custa R$ 15,00. O fazendeiro quer gastar, no máximo, R$ 6000,00 na compra de toda a tela necessária para o galinheiro, e deseja que o galinheiro tenha a maior área possível.
Qual será a medida, em metro, do maior lado do galinheiro?
A) 85
B) 100
C) 175
D) 200
E) 350
Resolução
A área do galinheiro é dada por
A = L.C
Além disso, o custo com a tela pode ser calculado pensando no perímetro desse galinheiro.
20.2L + 15.2C = 6 000
40L + 30C = 6 000
Simplificando essa equação temos
4L + 3C = 600
Para que a área seja a maior possível com 6000 de orçamento, o maior lado tem que ser o mais barato, ou seja, a incognta que acompanha o 15 reais por metro é a que a gente vai usar para fazer a equação de 2 grau.
Vamos então isolar uma incógnita nessa equação e substituir na equação da área
4L = 600 – 3C
L = (600-3C)/4
Daí,
A = (600-3C) . C/4
A = 600C/4 – 3C²/4
Como deseja-se que a área seja máxima, podemos descobrir o valor de C de maneira que seja A seja máximo, ou seja, descobrir o C do vértice (Xvértice= -b/2a)
b = 600/4
a = -3/4
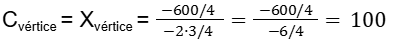
Alternativa B
Veja a resolução com mais detalhes no vídeo abaixo!
