Questão 147 – Análise Combinatória
Numa cidade, cinco escolas de samba (I, II, III, IV e V) participaram do desfile de Carnaval. Quatro quesitos são julgados, cada um por dois jurados, que podem atribuir somente uma dentre as notas 6, 7, 8, 9 ou 10. A campeã será a escola que obtiver maior pontuação na soma de todas as notas emitidas. Em caso de empate, a campeã será a que alcançar a maior soma das notas atribuídas pelos jurados no quesito Enredo e Harmonia. A tabela mostra as notas do desfile desse ano no momento em que faltava somente a divulgação das notas do jurado B no quesito Bateria.
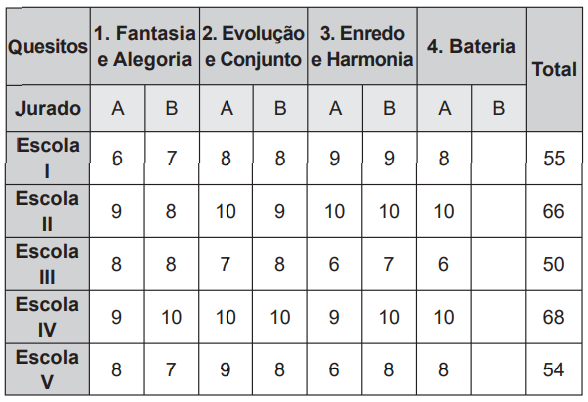
Quantas configurações distintas das notas a serem atribuídas pelo jurado B no quesito Bateria tornariam campeã a Escola II?
A) 21
B) 90
C) 750
D) 1 250
E) 3 125
Solução
Podemos observer que apenas as escolas II e IV podem ganhar, já que mesmo se elas ganhassem 0, elas ficariam em primeiro e segundo lugar.
Vamos então analisar cada caso em que a escola II é campeã, observando que se ocorrer empate, a escola II vence já que ganhou mais pontos na categoria 3:
Se a escola II tirar 10 ela fica com
66 + 10 = 76
O máximo que a escola IV pode tirar é 8 para que não ultrapasse a nota da II, nesse caso são três opções de notas a 6, 7 ou 8.
Se a escola II tirar 9 ela fica com
66 + 9 = 75
O máximo que a escola IV pode tirar é 7 para que não ultrapasse a nota da II, nesse caso são duas opções de notas a 6 ou 7.
Se a escola II tirar 8 ela fica com
66 + 8 = 74
O máximo que a escola IV pode tirar é 6 para que não ultrapasse a nota da II, nesse caso é 1 opção de nota.
No total são 3 + 2 + 1 = 6 configurações de notas
Devemos agora levar em consideração as outras escolas que tem cada uma 5 opções de notas que não vão interferir no resultado final, usando o princípio fundamental da contagem e considerando 3 escolas são no total
6.5.5.5 = 750 opções
Alternativa C






