Uma fatura mensal de água é composta por uma taxa fixa, independentemente do gasto, mais uma parte relativa ao consumo de água, em metro cúbico. O gráfico relaciona o valor da fatura com o volume de água gasto em uma residência no mês de novembro, representando uma semirreta.
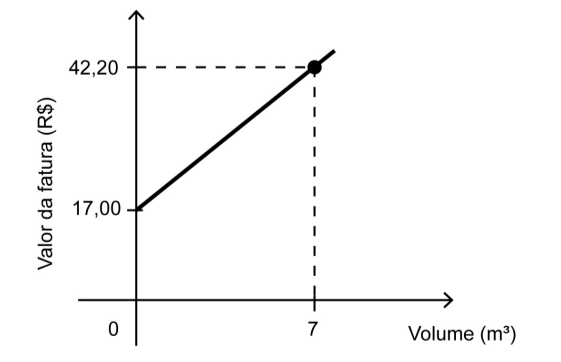
Observa-se que, nesse mês, houve um consumo de 7 m³ de água. Sabe-se que, em dezembro, o consumo de água nessa residência, em metro cúbico, dobrou em relação ao mês anterior.
O valor da fatura referente ao consumo no mês de dezembro nessa residência foi
A) superior a R$ 65,00 e inferior a R$ 70,00.
B) superior a R$ 80,00 e inferior a R$ 85,00.
C) superior a R$ 90,00 e inferior a R$ 95,00.
D) superior a R$ 95,00.
E) inferior a R$ 55,00.
Resolução
Nessa questão temos um gráfico de uma função do 1° grau, assim, sabemos que a função é f(x)=ax+b, para resolver podemos utilizar 2 pares ordenados (0,17) e (7, 42,20)
17 = 0x + b
42,20 = 7x + b
Multiplicando a primeira equação por (-1) temos:
-17= -b
42,20 = 7x +b
25,20 = 7x
25,20/7 = x
3,6 =x
Descoberto o x, basta substituir em uma das equações:
17 = 0*3,6 + b
17 = b
temos que a função que representa a reta é f(x) = 3,6x + 17
se o consumo dobrou ou seja, foi de 7m³ para 14 m³ basta substituir na equação para encontrar o valor da fatura:
f(x) = 3,6*14 + 17
f(x) = 50,4 + 17
f(x) = 67,4
Está entre 65,00 e 70,00
Alternativa A






