Questão 148 AMARELA – Progressão Aritmética
O triângulo da figura é denominado triângulo mágico. Nos círculos, escrevem-se os números de 1 a 6, sem repetição, com um número em cada círculo. O objetivo é distribuir os números de forma que as somas dos números em cada lado do triângulo sejam iguais.
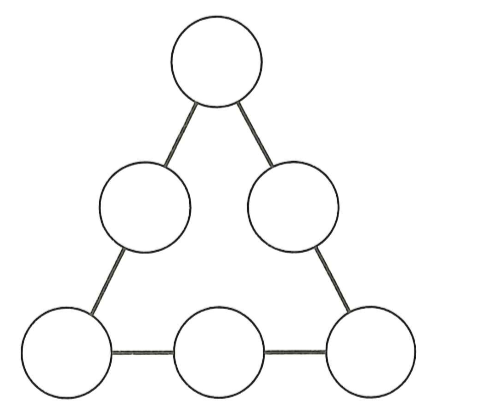
Considere que os números colocados nos vértices do triângulo estejam em progressão aritmética de razão igual a 2.
Nas condições propostas, quais as possíveis soluções para as somas dos números que formam os lados do triângulo?
A) Há somente uma solução possível, e as somas em cada lado do triângulo são iguais a 7.
B) Há somente uma solução possível, e as somas em cada lado do triângulo são iguais a 9.
C) Há somente duas soluções possíveis, uma em que as somas em cada lado do triângulo são iguais a 7 e outra em que as somas são iguais a 9.
D) Há somente duas soluções possíveis, uma em que as somas em cada lado do triângulo são iguais a 9 e outra em que as somas são iguais a 12.
E) Há somente duas soluções possíveis, uma em que as somas em cada lado do triângulo são iguais a 10 e outra em que as somas são iguais a 11.
Solução
Seja x o valor em um dos vértices, então os outros vértices terão x+1 e x+2.
Uma opção é x = 1, ou seja os vértices seriam 1,3 e 5.
Completando as somas para que sejam todos os lados iguais temos os lados com:
1,6 e 3, o outro 3,2,5, e o último 5,4 e 1. Esses lados a soma será 10.
Outra opção é x = 2, com vértices 2, 4 e 6. Onde Um lado terá os números:
2,5 e 4, o outro 4,1 e 6, e o último 2,3 e 6. Esses lados a soma será 11.
Temos só duas soluções possíveis. Já que x não pode ser maior que dois pois o ultimo vertice seria maior que 6.
Alternativa E
Veja a resolução com mais detalhes no vídeo abaixo!






