O Índice de Massa Corporal (IMC) pode ser considerado uma alternativa prática, fácil e barata para a medição direta de gordura corporal. Seu valor pode ser obtido pela fórmula
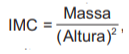
, na qual a massa é em quilograma e a altura, em metro. As crianças, naturalmente, começam a vida com um alto índice de gordura corpórea, mas vão ficando mais magras conforme envelhecem, por isso os cientistas criaram um IMC especialmente para as crianças e jovens adultos, dos dois aos vinte anos de idade, chamado de IMC por idade.
O gráfico mostra o IMC por idade para meninos.
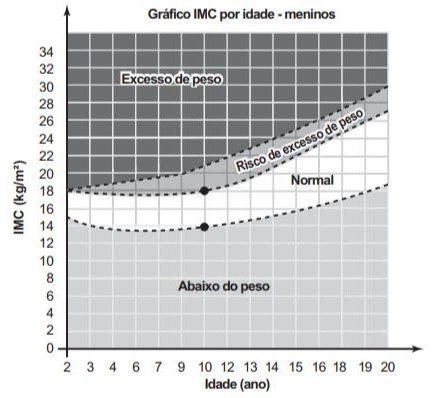
Uma mãe resolveu calcular o IMC do seu filho, um menino de dez anos de idade, com 1,20 m de altura e 30,92 kg.
Disponível em: http://saude.hsw.uol.com. Acesso em: 31 jul. 2012.
Para estar na faixa considerada normal de IMC, os valores mínimo e máximo que esse menino precisa emagrecer, em quilograma, devem ser, respectivamente
A) 1,12 e 5,12.
B) 2,68 e 12,28.
C) 3,47 e 7,47.
D) 5,00 e 10,76.
E) 7,77 e 11,77.
Solução
Conforme o gráfico, o maior IMC, ainda considerado normal, é igual a 18, e o menor igual a 14.
Portanto, basta substituir esses valores e encontrar quais os pesos máximo e mínimo que a criança pode atingir e fazer a diferença com o seu peso atual.
18 = X / 1,2²
X = 18 . 1,2² = 25,92 kg
14 = X / 1,2²
X = 14 . 1,2² = 20,16 kg
Fazendo as diferenças com o peso atual
D = 30,92 – 25,92 = 5 kg
D = 30,92 – 20,16 = 10,76 kg
Alternativa D






