Questão 150 – Geometria Analítica
Um bairro de uma cidade foi planejado em uma região plana, com ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho. No plano de coordenadas cartesianas seguinte, esse bairro localiza-se no segundo quadrante, e as distâncias nos eixos são dadas em quilômetros.
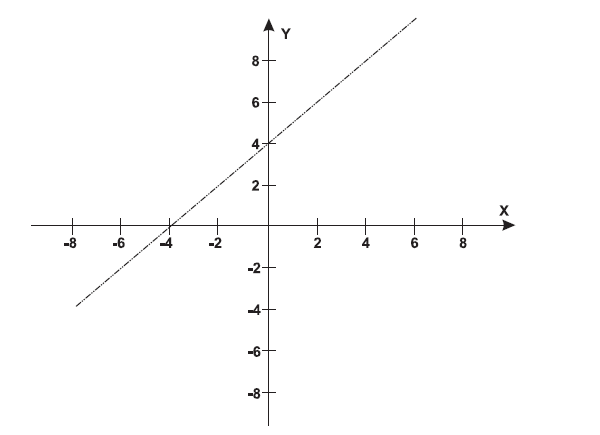
A reta de equação y = x + 4 representa o planejamento do percurso da linha do metrô subterrâneo que atravessará o bairro e outras regiões da cidade. No ponto P = (-5, 5), localiza-se um hospital público. A comunidade solicitou ao comitê de planejamento que fosse prevista uma estação do metrô de modo que sua distância ao hospital, medida em linha reta, não fosse maior que 5 km.
Atendendo ao pedido da comunidade, o comitê argumentou corretamente que isso seria automaticamente satisfeito, pois já estava prevista a construção de uma estação no ponto.
A) (–5, 0).
B) (–3, 1).
C) (–2, 1).
D) (0, 4).
E) (2, 6).
Solução
Devemos conferir quais pontos das alternativas satisfazem a equação.
(-5,0): ao substituir os valores em y = x + 4 teremos
0 = -5 + 4
0 = 1, que é falso, então não se encaixa na equação.
(-3,1): ao substituir os valores em y = x + 4 teremos
1 = -3 + 4
1 = 1, verdadeiro então se encaixa na equação.
(-2,1): ao substituir os valores em y = x + 4 teremos
1 = -2 + 4
1 = 2, que é falso então não se encaixa na equação.
(0,4):ao substituir os valores em y = x + 4 teremos
4 = 0 + 4
4 = 4, que é verdadeiro, então se encaixa na equação.
(2,6): ao substituir os valores em y = x + 4 teremos
6 = 2 + 4
6 = 6, que é verdadeiro, então se encaixa na equação.
Então devemos conferir se os pontos (-3,1), (0,4) e (2,6) tem distância menor ou igual a 5 do ponto (-5,5).
Vamos agora comparar um a um usando a fórmula de distância.
D = √[(x2 – x1)2 + (y2 – y1)2]
(-3,1):
D = √[(-5 – -3)2 + (5 – 1)2]
D = √[(-2)2 + (4)2]
D = √[4 + 16]
D = √20 = 4,47 que se encaixa já que é menor que 5.
(0,4):
D = √[(-5 – 0)2 + (5 – 4)2]
D = √[(-5)2 + (1)2]
D = √[25 + 1]
D = √26 = 5,09 que não se encaixa já que é maior que 5.
(2,6):
D = √[(-5 – 2)2 + (5 – 6)2]
D = √[(-7)2 + (-1)2]
D = √[49 + 1]
D = √50 = 7,07 que não se encaixa já que é maior que 5.
O único ponto que se encaixa em todas as características propostas é o ponto (-3,1).
Alternativa B






