Na construção de um avião de papel, uma criança dobrou uma folha retangular sobrepondo o lado DC ao lado AB. Assim, ela obteve dois novos retângulos, sendo um deles o retângulo DCNM, conforme a figura 1. Em seguida, ela fez uma nova dobradura, mantendo N fixo e sobrepondo o lado CN, de DCNM, a um segmento de MN. Essa sobreposição determinou um ponto P em MN e também um ponto Q em DC, conforme a figura 2.
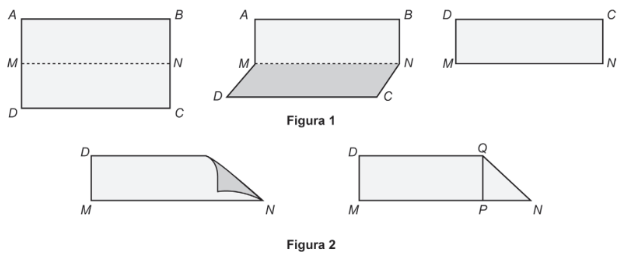
Considerando as classificações quanto à medida dos ângulos e à medida dos lados, o triângulo NPQ é
A) acutângulo e escaleno.
B) acutângulo e isósceles não equilátero.
C) acutângulo e equilátero.
D) retângulo e escaleno.
E) retângulo e isósceles não equilátero.
Solução
Nessa questão basta visualizar que o lado CN do retângulo representa a largura do retângulo e, ao ser dobrado para formar o triângulo, passa a ser nomeado como o lado PN do triângulo. Sendo assim, podemos notar que PN tem a mesma medida que CN e, consequentemente, PN tem a mesma medida que QP, pois ao fazer a dobradura QP, também, passa a representar a largura do retângulo. Com isso, sabemos que o triângulo NPQ, tem 2 lados iguais, sendo então, um triângulo isósceles.
Além disso, sabe-se que o ângulo formado com dois lados de um retângulo, formam 90º, com isso, pode-se concluir também que o ângulo em P, é 90º.
Portanto, o triângulo obtido NPQ é retângulo e isósceles, não sendo equilátero, pois a hipotenusa no triângulo retângulo é maior que os dois catetos.
Alternativa E






