Questão 152 – Função Trigonométrica
Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra. Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por
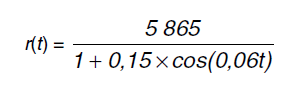
Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
O cientista deveria concluir que, periodicamente, S atinge o valor de
A) 12 765 km.
B) 12 000 km
C) 11 730 km
D) 10 965 km.
E) 5 865 km.
Solução
Analisando r(t), como a função cos(0,06t) está no denominador, isso significa que o maior valor de cos(0,06t) corresponde ao menor valor da função r(t).
O maior valor possível de cos(0,06t) = 1, então vamos substituir na equação para descobrir o valor mínimo de r
rmin = 5865/(1 + 0,15.1) = 5865/1,15 = 5100 km
O menor valor possível de cos(0,06t) = -1, então vamos substituir na equação para descobrir o valor máximo de r
rmax = 5865/(1 + 0,15.-1) = 5865/0,85 = 6900 km
Somando
S = 5100 + 6900 = 12000 km
Alternativa B
