Questão 152 – Função de 2º Grau
Para a comunicação entre dois navios é utilizado um sistema de codificação com base em valores numéricos. Para isso, são consideradas as operações triângulo e estrela *, definidas sobre o conjunto dos números reais por xΔy = x² + xy – y² e x * y = xy + x.
O navio que deseja enviar uma mensagem deve fornecer um valor de entrada b, que irá gerar um valor de saída, a ser enviado ao navio receptor, dado pela soma da duas maiores soluções da equação (aΔb)*(bΔa) = 0. Cada valor possível de entrada e saída representa uma mensagem diferente já conhecida pelos dois navios.
Um navio deseja enviar ao outro a mensagem “ATENÇÃO!”. Para isso, deve utilizar o valor de entrada b=1.
Dessa forma, o valor recebido pelo navio receptor será
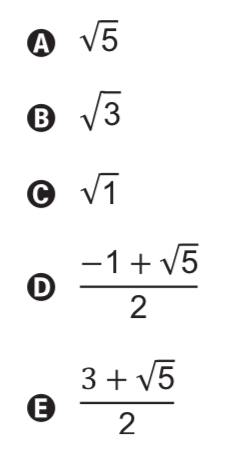
Solução
Sendo b = 1,
(aΔb)*(bΔa) = (aΔ1)*(1Δa)
Pelas propriedade apresentadas
(aΔ1)*(1Δa) = (a² + 1.a – 1²)*(1² + 1.a – a²)
(a² + a – 1).(1 + a – a²) = (a² + a – 1).(1 + a – a²) + (a² + a – 1)
(a² + a – 1).(1 + a – a²) + (a² + a – 1) = (a² + a – 1).[(1 + a – a²) + 1]
(a² + a – 1).[(1 + a – a²) + 1] = (a² + a – 1).(2 + a – a²)
Se (aΔ1)*(1Δa) = 0
então
(a² + a – 1).(2 + a – a²) = 0
Para que a multiplicação acima seja igual a zero temos duas opções:
a² + a – 1 = 0 ou – a² + a + 2 = 0
Vamos calcular qual valor de a satisfaz cada equação usando bhaskra
1º) a² + a – 1 = 0
Δ = 1 + 4 = 5
a = (-1 +- √5)/2
a1 = (-1 + √5)/2
a2 = (-1 – √5)/2
2º) -a² + a + 2 = 0
Δ = 1 + 8 = 9
a = (1 +- √9)/2
a3 = (1 + 3)/2 = 2
a4 = (1 – 3)/2 = -1
O enunciado nos diz que a mensagem enviada é a soma das duas maiores soluções que nesse caso são a1 e a3.
(-1 + √5)/2 + 2 = (3 + √5)/2
Alternativa E
Veja a resolução com mais detalhes no vídeo abaixo!






