Questão 153 – Geometria Espacial
Suponha que, na escultura do artista Emanoel Araújo, mostrada na figura a seguir, todos os prismas numerados em algarismos romanos são retos, com bases triangulares, e que as faces laterais do poliedro II são perpendiculares à sua própria face superior, que, por sua vez, é um triângulo congruente ao triângulo base dos prismas. Além disso, considere que os prismas I e III são perpendiculares ao prisma IV e ao poliedro II.
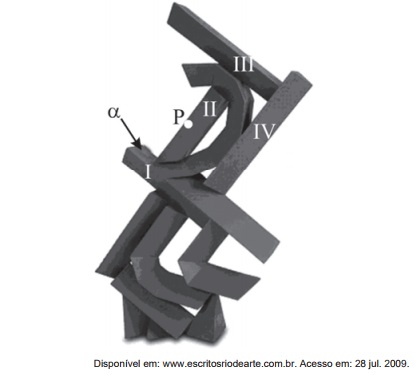
Imagine um plano paralelo à face α do prisma I, mas que passe pelo ponto P pertencente à aresta do poliedro II, indicado na figura. A interseção desse plano imaginário com a escultura contém
A) dois triângulos congruentes com lados correspondentes paralelos.
B) dois retângulos congruentes e com lados correspondentes paralelos.
C) dois trapézios congruentes com lados correspondentes perpendiculares.
D) dois paralelogramos congruentes com lados correspondentes paralelos.
E) dois quadriláteros congruentes com lados correspondentes perpendiculares.
Solução
O corte é paralelo a barra I, consequentemente será perpendicular ao poliedro II e ao prisma IV, então ao cortar será formado exatamente o triângulo das extremidades que são congruentes.
Por II e IV serem paralelos, os triângulos também terão lados correspondentes paralelos.
Alternativa A






